Теория вероятностей. Преобразование случайных величин.

[Urcaserem]

Здравствуйте! У меня очередная задача по теории вероятностей.
Случайная величина $\xi$ распределена равномерно на отрезке $[0;\pi]$. Найти закон распределения СВ $\eta=\sin\xi$.
Плотность для $\xi$ я нашла.
Функция распределения у меня получилась

$$\begin{cases} 0,&\text{если $y\leqslant0$;}\\ \tfrac{2}{\pi} \arcsin y ,&\text{если $0<y\leqslant1$;}\\ 1,&\text{если $1\leqslanty$.} \end{cases}$$

У меня вопрос. Правильно ли я нашла закон распределения?

Я нарисовала график синуса. Потом провела прямую $y$ (параллельно оси $x$) и посмотрела, где график синуса лежит под этой прямой. Оказалось, что на отрезке $[0;\arcsin y]$ и на $[\pi- \arcsin y;\pi]$. Они одинаковой длины. Потом умножаю $\frac{1}{\pi}$ ( плотность распределения на этих отрезках ) на длину этих отрезков.

Правилен ли ход моего решения?
я просто не уверена насчёт последнего действия. Я просто запоролась однажды примерно на такой задаче, и решала неправильно с помощью формулы для строго монотонной функции, а у меня не монотонная...

[Mihr]

Функцию распределения Вы нашли правильно, но в представленной Вами записи этой функции есть ошибка (очевидно, механическая). Посмотрите сами на 3-ю строчку записи справа от фигурной скобки ("1, если 1").

[Urcaserem]

Mihr
Ой, ну конечно, если $y>1$
Я, собственно, наверно не до конца поняла, почему плотность нужно умножать на длину отрезка.
Это площать под графиком? Плотности

[Mihr]

Urcaserem, я не уверен, что понимаю Ваше решение, просто вижу, что ответ правильный Сам я решаю подобные задачи иначе. Поэтому никаких комментариев к Вашему решению давать не рискну. Давайте подождём: может, кто из математиков форума выскажется. Так будет, я думаю, лучше.

[Urcaserem]

Mihr
Да, подождем
А Ваш способ решения кординально отличается от моего?

[mihaild]

Да, всё правильно. Вам нужно найти $P(\eta < y)$, это ровно мера множества $\eta^{-1}([0; y])$ относительно $\xi$. Вы нашли само множество $\eta^{-1}([0; y])$ - это как раз ваши два отрезка. Теперь нужно найти меру этих отрезков относительно $\xi$. А чему равна мера отрезка относительно равномерного распределения на каком-то отрезке длины $a$? Она равна длине этого отрезка, деленной на $a$, если отрезок целиком лежит в носителе, и нулю, если с носителем не пересекается (а если пересекается, но не лежит, то понятно как разбивать) - это просто определение равномерного распределения.

Или иначе - вам на самом деле нужно не умножить плотность на длину, а проинтегрировать её по отрезку. Но т.к. плотность постоянная - то интеграл как раз оказывается равным произведению плотности на длину отрезка.

[Mihr]

(Оффтоп)

Urcaserem, ну вот, Вам уже ответили, замечательно. Я решаю аналитически, без "геометрических соображений". Могу, конечно, изложить, но, думаю, для Вас сейчас это лишнее. Если Вы готовитесь к экзаменам, для Вас лучше понять прежде всего тот способ, который Вам излагали. Чтобы не было потом взаимного непонимания студента и преподавателя на экзамене (такое, как ни крути, случается).

[Urcaserem]

Я просто интересовалась (давно) , после первой неудачи как решать у преподавателя, которого дико боюсь, и когда он говорил мной, я могла часть пропустить и не понять, из того что я помню получился верный ответ
У меня в памяти всплывает, что он говорил, найдешь отрезки , где функция (график) лежит под прямой $y$ (это точно) и вот у тебя есть плотность на этих отрезках (тоже прямая) и вероятность будет равно площади под эти графиком (прямоугольник со сторонами равной плотности и найденного отрезка), а вот этт уже неточно .... что-то могла наврать

-- 04.01.2020, 23:54 --

Оооой, пока я строчила, мне ответили!!

Да, я припоминаю, что подобное что и mihaild
мне говорил преподаватель!
Просто от смущения что-то не воспринималось, да и давно было...

Спасибо , я всё поняла!!

-- 05.01.2020, 00:11 --

Mihr
Если честно, то мне интересно, как можно аналитически это решить , может мне даже легче будет.
Если вам не трудно, поделитесь в свободное время? Это уже моё любопытсво

[Mihr]

Urcaserem, хорошо, постараюсь завтра написать.

[Mihr]

Urcaserem, итак, если Вам интересно, моё решение.

1. Как я решал на самом деле.

а) Разбиваем данный отрезок $[0;\pi]$ (где плотность распределения отлична от нуля) на промежутки монотонности данной нам функции $y=\sin x$, то есть, на отрезки $[0;\frac{\pi}{2}]$ и $[\frac{\pi}{2};\pi]$ (на первом из этих отрезков функция $\varphi (x)=\sin x$ строго возрастает, на втором - строго убывает). На каждом из этих отрезков строим обратную функцию: $\varphi_1^{-1} (y)=\arcsin y$ на первом отрезке и $\varphi_2^{-1} (y)=\pi-\arcsin y$ - на втором отрезке.

б) Вычисляем плотность итогового распределения так:

$$g(y)=f(\varphi_1^{-1} (y))\left\lvert \dfrac{d}{dy}\varphi_1^{-1} (y)\right\rvert + f(\varphi_2^{-1} (y))\left\lvert \dfrac{d}{dy}\varphi_2^{-1} (y)\right\rvert$$

(За обоснованием этой формулы отсылаю к книге: И.П. Мацкевич, Г.П. Свирид. Высшая математика. Теория вероятностей и математическая статистика. Минск, 1993, с. 40-42. Там, правда, несколько иные обозначения, но разобраться в них несложно. Подчеркну от себя, что в данном случае задача немного упрощается из-за того, что на обоих промежутках монотонности функция $\varphi (x)=\sin x$ имеет одно и то же множество значений - отрезок $[0;1]$.)
В нашем случае:

$$g(y)=\dfrac{1}{\pi}\left\lvert \dfrac{d}{dy}\arcsin y\right\rvert + \dfrac{1}{\pi}\left\lvert \dfrac{d}{dy}(\pi-\arcsin y)\right\rvert=\dfrac{1}{\pi}\left\lvert \dfrac{1}{\sqrt{1-y^2}}\right\rvert + \dfrac{1}{\pi}\left\lvert -\dfrac{1}{\sqrt{1-y^2}}\right\rvert$$

Таким образом,

$$g(y)=\dfrac{2}{\pi} \dfrac{1}{\sqrt{1-y^2}}$$

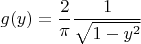
в) Интегрируя полученный результат, находим функцию распределения (там, где плотность распределения отлична от нуля):

$$G(y)=\int\limits_{0}^{y} g(t)dt=\int\limits_{0}^{y} \dfrac{2}{\pi} \dfrac{dt}{\sqrt{1-t^2}}=\dfrac{2}{\pi} \arcsin y$$

Если Вы так никогда не решали, то, скорее всего, для Вас сейчас это выглядит сложновато, но здесь, как говорится, вопрос привычки. Для меня просто так привычнее.

2. Как это можно было бы решить попроще.

Строим предварительно функцию распределения случайной величины $\xi$:

$$F(x)=\int\limits_{0}^{x}\dfrac{1}{\pi}dx=\dfrac{x}{\pi}$$

Строим теперь функцию распределения случайной величины $\eta$, исходя из определения функции распределения:

$$G(y)=P(\eta<y)=P(\sin \xi<y)=P(\xi<\arcsin y \vee \xi>\pi-\arcsin y)=P(\xi<\arcsin y)+P(\xi>\pi-\arcsin y)$$

Последнее равенство здесь основано на теореме о вероятности суммы несовместных событий.
Возвращаемся теперь от вероятностей обратно к функции распределения:

$$G(y)=F(\arcsin y)+1-F(\pi-\arcsin y)=\dfrac{1}{\pi}\arcsin y+1-\dfrac{1}{\pi}(\pi-\arcsin y)=\dfrac{2}{\pi}\arcsin y$$

Ещё раз: если написанное выше плохо понятно, лучше сейчас не тратьте время на разбор этого текста. Готовьтесь отвечать так, как Вас учили. Будет время и желание вникнуть - вернётесь к этой странице после сессии. Успехов.

[Sicker]

Urcaserem
На будущее
В случае монотонной функции плотность распределения случайно величины $y=f(x)$ с плотностью распределения аргумента $\rho(x)$ равна $\xi(y)=\frac{\rho (f^{1} (y))}{f'(f^{-1}(y))}$

[Urcaserem]

Sicker
Спасибо
Mihr
Мне не показалось сложнее, даже понятнее мне было бы ,если изначально объясняли так. Формулами я этими пользовалась только для строго монотонных функций:)
Спасибо вам огромное!)