Добавлю ещё что меня поразило: доказательство что комплексные числа являются таким "последним из могикан", не расширяемы дальше без потери каких-то важных свойств. Т.е. ряд последовательных расширений понятий "натуральные - целые - рациональные - действительные - комплексные" на них и обрывается, дальше его не продолжить.
Не на комплексных, а на действительных. Действительные числа - это максимальное
упорядоченное поле, то есть в нём выполняются аксиомы поля (см. определение поля в алгебре) и есть отношение сравнения

, согласованное с этими операциями привычным образом.
На комплексных же числах нельзя ввести операцию сравнения так, чтобы из

следовало

, и для

числа

и

были разных знаков.
(Доказательство)
Предположим, что такая операция введена. Рассмотрев произвольное

, видим, что

(если
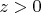
, то как

, а если

, то как

). В частности,

и

. Т.е.

и

получаются одного знака. Противоречие.