Н.С.Пискунов в "Дифференциальное и интегральное исчисление", Т.1, глава IX писал(а):
...
![$$\[\dfrac{1}{R^2}=\Big(\dfrac{d^2\mbox{\boldmath$r$}}{ds^2}\Big)^2\eqno(6)\]\\$$ $$\[\dfrac{1}{R^2}=\Big(\dfrac{d^2\mbox{\boldmath$r$}}{ds^2}\Big)^2\eqno(6)\]\\$$](https://dxdy-04.korotkov.co.uk/f/b/4/e/b4ebe93dedf381fe14fc36e99d14c82f82.png)
...
Рассмотрим случай, когда радиус-вектор

выражен как функция произвольного параметра

:

В этом случае длину дуги

будем рассматривать как фукнцию параметра

. Тогда вычисление кривизны производится следующим образом:
![$$\[\dfrac{d\mbox{\boldmath$r$}}{dt}=\dfrac{d\mbox{\boldmath$r$}}{ds}\dfrac{ds}{dt}\eqno(7)\]\\$$ $$\[\dfrac{d\mbox{\boldmath$r$}}{dt}=\dfrac{d\mbox{\boldmath$r$}}{ds}\dfrac{ds}{dt}\eqno(7)\]\\$$](https://dxdy-01.korotkov.co.uk/f/c/a/8/ca8198e5a0c2e733e336e5a9c3a4600c82.png)
Так как

то
![$$\[\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2=\Big(\dfrac{ds}{dt}\Big)^2\eqno(8)\]\\$$ $$\[\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2=\Big(\dfrac{ds}{dt}\Big)^2\eqno(8)\]\\$$](https://dxdy-02.korotkov.co.uk/f/9/b/c/9bc2b17b756cc567c78a3156baf4968b82.png)
Дифференцируя правую и левую части и сокращая на два, получим:
![$$\[\dfrac{d\mbox{\boldmath$r$}}{dt}\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}=\dfrac{ds}{dt}\dfrac{d^2s}{dt^2}\eqno(9)\]\\$$ $$\[\dfrac{d\mbox{\boldmath$r$}}{dt}\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}=\dfrac{ds}{dt}\dfrac{d^2s}{dt^2}\eqno(9)\]\\$$](https://dxdy-04.korotkov.co.uk/f/7/9/b/79be4a76564860fc8d0e2875f905697882.png)
Далее, из формулы (7) следует:

Дифференцируем по

обе части последнего равенства:

Подставляя полученное выражение
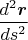
в формулу (6), будем иметь:
![$$\dfrac{1}{R^2}=\Bigg[\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\dfrac{1}{\Big(\dfrac{ds}{dt}\Big)^2}-\dfrac{d\mbox{\boldmath$r$}}{dt}\dfrac{\dfrac{d^2s}{dt^2}}{\Big(\dfrac{ds}{dt}\Big)^3}\Bigg]^2=
\dfrac{\Big(\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\Big)^2\Big(\dfrac{ds}{dt}\Big)^2
-2\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\dfrac{d\mbox{\boldmath$r$}}{dt}\dfrac{ds}{dt}\dfrac{d^2s}{dt^2}
+\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2\Big(\dfrac{d^2s}{dt^2}\Big)^2} {\Big(\dfrac{ds}{dt}\Big)^6}$$ $$\dfrac{1}{R^2}=\Bigg[\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\dfrac{1}{\Big(\dfrac{ds}{dt}\Big)^2}-\dfrac{d\mbox{\boldmath$r$}}{dt}\dfrac{\dfrac{d^2s}{dt^2}}{\Big(\dfrac{ds}{dt}\Big)^3}\Bigg]^2=
\dfrac{\Big(\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\Big)^2\Big(\dfrac{ds}{dt}\Big)^2
-2\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\dfrac{d\mbox{\boldmath$r$}}{dt}\dfrac{ds}{dt}\dfrac{d^2s}{dt^2}
+\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2\Big(\dfrac{d^2s}{dt^2}\Big)^2} {\Big(\dfrac{ds}{dt}\Big)^6}$$](https://dxdy-04.korotkov.co.uk/f/b/e/f/befad290c60c268176a55bbfc5f5deac82.png)
Выражая

и

по формулам (8) и (9) через производные от

, получим:
![$$\[\dfrac{1}{R^2}=
\dfrac{\Big(\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\Big)^2\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2
-\Big(\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2} {\Big[\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2\Big]^3}\eqno(10)\]\\$$ $$\[\dfrac{1}{R^2}=
\dfrac{\Big(\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\Big)^2\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2
-\Big(\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2} {\Big[\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2\Big]^3}\eqno(10)\]\\$$](https://dxdy-01.korotkov.co.uk/f/0/3/8/038e5d7fe872c248648d832c250aa17382.png)
Не понимаю, как из предпоследнего выражения получается формула (10).
Попробуем преобразовать слагаемые числителя в предпоследнем выражении с учетом формул (8) и (9).
Первое слагаемое:

Второе слагаемое:

Третье слагаемое:

В итоге получается:
![$$\dfrac{1}{R^2}=
\dfrac{2\Big[\Big(\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\Big)^2\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2
-\Big(\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2\Big] }{\Big[\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2\Big]^3}$$ $$\dfrac{1}{R^2}=
\dfrac{2\Big[\Big(\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\Big)^2\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2
-\Big(\dfrac{d^2\mbox{\boldmath$r$}}{dt^2}\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2\Big] }{\Big[\Big(\dfrac{d\mbox{\boldmath$r$}}{dt}\Big)^2\Big]^3}$$](https://dxdy-01.korotkov.co.uk/f/c/1/2/c12ef0733e918db9965325cbeeebb8d682.png)
Не пойму, где ошибся и откуда вылезла двойка.



