...Продолжу.
Возьмем задачу о сумме подмножеств.
У нас есть

чисел и

комбинаций этих чисел.
Нам нужно среди этих комбинаций найти одну удовлетворяющую определенному условию (равенству числу)путь это будет число

.
Можно свести эту задачу к не сортированному списку, для этого избавимся от всех чисел:
Для этого мы берем первое число

и делим задачу на 2 под задачи:
1)В первой подзадаче мы будем использовать первое число - то есть мы его вычтем из

- Условие у нас будет равно
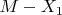
.
2)Во второй подзадаче мы не будем использовать первое число. И поэтому условие так и остается равенство

.
Таким образом мы избавились от числа

В этих двух случаях.
Проделав то же самое для остальных

чисел мы получим не сортированный список из

позиций.
И задача о сумме подмножеств сведется к поиску одного верного равенства из не сортированного списка равенств.
Теперь о задаче поиска по не сортированному списку.. Для этого представим другую задачу:
У нас есть колода карт лежащая рубашкой вверх. Нам нужно в этой колоде найти пиковую даму. Все что мы можем - это последовательно брать сверху по одной карте и смотреть что это за карта.Можем ли мы избавиться более чем от одной карты за 1 действие?
Нет. Потому что расположение карт в колоде для нас неизвестно. Поэтому неизвестные карты для нас равнозначны.
Мы так же можем в любой момент перетасовать колоду. Но это ничего не изменит - верхняя карта колоды как была для нас неизвестной так и останется.
Но если бы бы колода была бы отсортирована - мы могли бы применить алгоритм быстрого бинарного поиска и найти искомое.
Точно так же в задаче о сумме подмножеств - мы не будем знать чему будет равна сумма нескольких чисел пока её не посчитаем.
Мы не будем знать точный ответ пока не посчитаем все суммы. Так как каждая из них может удовлетворять равенству.
...
Да, всё вычислимое на детерминированной машине вычислимо и на недетерминированной и наоборот, но за разное число шагов. Сведение недетерминированной МТ к детерминированной в худшем случае экспоненциально замедляет время вычисления, а экспонента от непостоянного полинома уже не полином.
Ну то есть вопрос равенства


можно свести к вопросу: "возможно ли существование недетерминированной машины Тьюринга?" ??
пожалуй подумаю над этим...