Рассмотрим параболическую задачу в области

с нелинейным граничным условием (остывающий сам по себе стержень подогревается с правого конца в зависимости от средней температуры; при этом возможны некоторые колебания, зависящие от времени):

где

,

и

непрерывные и достаточно гладкие,

монотонна по второй переменной:

при всех
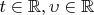
. Будем также считать, что

и

имеют период

по

.
Меня интересует корректность (существование, единственность решений задачи Коши

, непрерывная зависимость от н. д. и продолжимость на бесконечный промежуток

) в пространстве

. Прошу помочь ссылками на литературу.
Наиболее близкая работа, которую мне удалось найти: Arrieta J. M., Carvalho A. N., Rodríguez-Bernal A. Attractors of parabolic problems with nonlinear boundary conditions. Uniform Bounds //Communications in Partial Differential Equations, 25, 1-37 (2000).
Ее недостатки для моих нужд:
1). Рассматривается только автономный случай. 2). Их граничное условие

не допускает возможность использования средней температуры, а позволяет использовать только значение на концах стержня.
Множество других работ по нелинейным граничным задачам, которые не буду упоминать, также обладает недостатком 2), но к тому же еще зачастую рассматривает корректность не в

, а в каких-нибудь соболевских пространствах.



