Доброго времени суток, уважаемые форумчане.
В процессе поисков интересных задач наткнулся на любопытный образчик, который представляю вашему вниманию.
Цитата:
Найти все значения параметра

, при которых уравнение

имеет два различных корня, принимая в расчёт, что параметр

может быть только натуральным числом.
- Сначала необходимо упростить выражение в левой части уравнения:




- В итоге получилось квадратное уравнение вида
 , где в рассматриваемом случае
, где в рассматриваемом случае 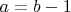 ,
,  ,
,  .
. - Известен факт, что у квадратного уравнения есть два различных корня, если дискриминант его квадратного трёхчлена положителен. Следовательно, для решения задачи необходимо найти дискриминант
 квадратного трёхчлена уравнения и затем решить неравенство
квадратного трёхчлена уравнения и затем решить неравенство  для нахождения
для нахождения  , удовлетворяющих условию.
, удовлетворяющих условию. - Дискриминант полученного при первом шаге квадратного трёхчлена вычисляется по формуле
 . После подстановки значений для
. После подстановки значений для  ,
,  и
и  необходимо раскрыть скобки и привести подобные:
необходимо раскрыть скобки и привести подобные:






- Теперь необходимо решить неравенство
 .
.

Произведение двух множителей больше нуля тогда и только тогда, когда у этих множителей одинаковые знаки - или они оба положительные, или они оба отрицательные. Так как  (положительное число), то выражение
(положительное число), то выражение  также должно быть больше нуля. Чтобы это выполнялось,
также должно быть больше нуля. Чтобы это выполнялось,  должно быть меньше двух. Но раз у нас
должно быть меньше двух. Но раз у нас  - натуральное число, то значение, удовлетворяющее такому неравенству, только одно: единица.
- натуральное число, то значение, удовлетворяющее такому неравенству, только одно: единица.
Казалось бы, можно брать и записывать ответ, но если мы поставим единицу в исходное уравнение, тогда получится, что его дискриминант будет равен нулю, следовательно, будет один корень.
Прошу помощи в нахождении ошибки в моём рассуждении - вроде бы, всё логично, а результат на выходе неверный.
С уважением,
-Exp.