Но всё ж таки скрытые проблемки остаются. Я ради интереса перебрал сочетания

с шагом 0,1. Если я нигде не ошибся в коде, то картинка соответствует значению действительной части наибольшего корня. Заметно, что область "гурвицевости" (синие оттенки) получается довольно хитрая.
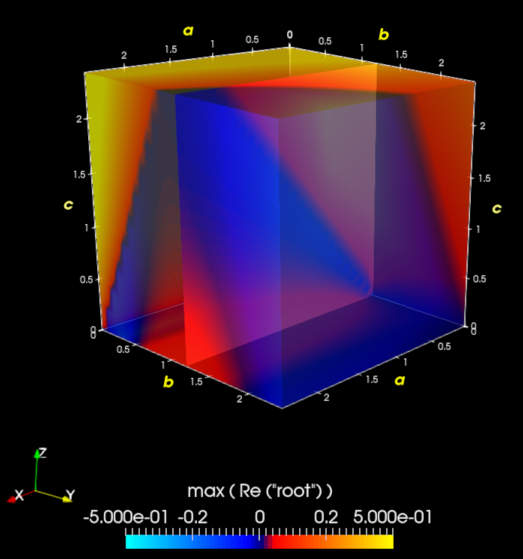
Неподвижная картинка не очень удобна - она лучше работает, когда её можно крутить мышью, делать "вырезки" из середины и прочее.
Если захочется проверить самостоятельно, то я использовал следующую технологию (использованные программы - open-source, свободно гуглятся и скачиваются). Корни многочлена и наибольшая действительная часть корня вычислялись в Maxima. Счёт занимает около минуты. Программка создаёт CSV-файл из 4-х полей:

и наибольшая из действительных частей корня. Файл был загружен в Paraview и получен цветной кубик. Это уже без всяких скриптов, просто щелчками мыши по желаемым кнопочкам и палитрам. На худой конец, даже Excel принимает CSV и может строить объёмные графики. Возможности у него не особо широкие, но лучше, чем ничего.
Код "Maxima"
Код:
/* Исследуемый показатель: наибольшая из действительных частей корней заданного многочлена */
poly(a,b,c):=x^5 +a*x^4 +2*(1+b)*x^3 +a*(1+b)*x^2 +4*b*x +(a*b-c)$
krit(a,b,c):=apply(max,map(lambda([x],realpart(rhs(x))),
allroots(poly(a,b,c))))$
mystep:0.1$
mybound:2.5$
with_stdout("roots.csv",
for a:0 step mystep while a<=mybound do
for b:0 step mystep while b<=mybound do
for c:0 step mystep while c<=mybound do
printf(true,"~8,5f,~8,5f,~8,5f,~8,5f~%",
a,b,c, krit(a,b,c)));



