Разве что

и нельзя делить на ноль.
Именно поэтому. В целом, моя мысль была проста: циклическая структура

дает дополнительные возможности при вычислениях в конечных полях.
Что можно было бы делать дальше?
1. Привыкнуть к тому, что

есть векторное пространство над

(это чуть побогаче, чем просто изоморфизм аддитивной группы поля

и прямой суммы нужного количества экземпляров

). Бонусы: линейные зависимости/независимости, базисы, ранги, подпространства, линейные операторы и т.п. бесплатно.
2. Подсчет всего, что можно подсчитать (в принципе, в

все конечно). Например: чему равно количество подпространств данной размерности (кажется, этим летом Вы начинали это занятие, но до конца не довели). Это элементарная комбинаторика.
3. Некоторые подпространства оказываются подполями (т.е. замкнуты не только относительно сложения, но и умножения тоже). Разобраться с этим. Почувствовать, например, что

не содержит внутри себя
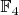
(только
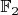
).
4. Да, а умеем ли мы построить поле

? Освоить конструирование конечных полей и арифметические действия в них.
5. Начать потихоньку грызть Лидла и Нидеррейтера. Там прорва упражнений на любой вкус и цвет. Одна из ближайших (а может, и не очень) морковок: нелинейная (в общем случае) задача факторизации многочленов становится линейной над конечным полем. (Prerequisites: нужно актуализировать теорию многочленов; в частности, свыкнутся с мыслью, что многочлен это не функция.)