Читая физическую литературу, столкнулся с математическим утверждением касательно уравнения, которое для полноты картины набью:

"Это линейное неоднородное уравнение относительно

. Согласно общему правилу такое уравнение имеет решение лишь в том случае, если правая часть ортогональна решению соответствующего однородного уравнения с теми же граничными условиями. Эти условия заключаются в обращении

в нуль на

. "
Мне непонятно, о каком общем правиле идёт речь. Я себе представляю это так: пусть есть линейный оператор

и однородное уравнение с этим оператором, имеющее решение

:

Пусть также есть задача с тем же оператором и теми же гран. условиями, но с правой частью

:

И в этой ситуации, если я верно понимаю, необходимо доказать, что

Чисто интуитивно можно было бы записать это скалярное произведение в таком виде
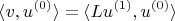
И вот тут-то, если бы рассматриваемый оператор был эрмитов, можно бы было перекинуть его действие с эрмитовым сопряжением на второй аргумент, на эрмитово сопряжение "забить" и получить

Что и требовалось. Выходит, упомянутое "общее правило" такое - для эрмитова оператора элементы его ядра ортогональны образу? Но тогда не очень понятно - про эрмитовость в книжке не упомянуто, хотя и получить её можно (эрмитовость второй производной на пространстве достаточно гладких функций с спаданием на плюс-минус бесконечности доказывается, остальные входящие в оператор слагаемые - число или вещественнозначная функция, итого эрмитов). Да и само "общее правило" - это выходит что-то на тему теоремы Фредгольма?

Тут можно для эрмитового заменить

на

и получить желаемое. Действительно ли автор имел в виду это, описывая "общее правило" или я давно потерял с ним контакт?



