Вы ерунду какую-то пишите
А, точно. Там нужно было написать не
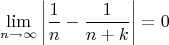
А

Причем, обратите внимание, там, в критерии Коши есть такая А перевернутая вверх лапками перед мэ. Это означает, что для критерия это должно выполняться для любого мэ, а не только для

при заранее заданном

Я похоже вот это не понял. Думал для любого означает, что могу взять

и

, тогда какое бы

бы мне не дали, я бы брал
![$n=[\frac{1}{\varepsilon}]+1$ $n=[\frac{1}{\varepsilon}]+1$](https://dxdy-02.korotkov.co.uk/f/1/e/1/1e1fb3a64335c4bede24b4414ff1f03582.png)
и в ус не дул. А для любого это означает, что должно выполняться и для

и для

, и для

?
Ну конечно, тогда бы это не называлось для любого... Ладно, нужно было подольше подумать, всем большое спасибо!!!