Цитата:
ещё один важный множитель, сдвигающий ответ
Там 2 ответа:

и

,— которые сдвинуты по-разному относительно моих

и

. Нужен множитель

в экспоненте.
Фейнман в дальнейших рассуждениях умножает на скорость (формула 40.6):

Т.е. переводит из количества молекул на ед. объема в количество, достигающее ед. площади за ед. времени., т.к.

— число молекул в ед. объема со скоростью

,

— число молекул со скоростью

, достигающих поверхности с одной стороны (отсюда

) за ед. времени.
Количество молекул , проходящее в ед. времени через единицу площади ,

выражается через число молекул в ед. объема

следующим образом:


,
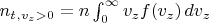

.
Если разделить 2 последних уравнения, то получим то же, что у Фейнмана

. Причем

— минимально возможная энергия этих молекул. Получается, распределение по двум другим осям не имеет значения.
-- 29.09.2019, 14:59 --Там ответ соответствуют просто распределению по энергиям.
И как его получить?