Простая задача на нахождение предела.
Цитата:

с
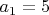
Найдите вещественнозначную функцию

, задающую эту последовательность, то есть

. Исследуя функцию

и её производные, докажите, что последовательность

ограниченна и монотонна. Объясните, почему предел

должен существовать.
Я, конечно, могу найти предел, он равен

, но я не понимаю, какой смысл имеет

и чем интересны её производные. Я могу доказать, что последовательность нестрого убывает на интервале
![$[2, 6]$ $[2, 6]$](https://dxdy-04.korotkov.co.uk/f/f/9/a/f9ab2956616804140058288c011f998f82.png)
, просто исследовав разницу

Что имелось в виду в подсказке?