Добрый день! Не очень понимаю - как определять достаточные условия экстремума функции двух переменных через градиент.
На семинаре разбирали такое задание:
Найти экстремум функции двух переменных.

при условии

Как методом Лагранжа нашли точки

при
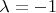
и точку
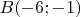
при

я хорошо понимаю. Но дальше вместо окaймлeннoго Гессиaнa почему-то стали смотреть как там ведет себя градиент

. А дальше нарисовали график

, отметили точку

, в ней нарисовали градиент

и дальше исходя из графика сделали вывод - что точка

- есть точка максимума. Но почему? Как? Нужны детали. Хочу разобраться! Помогите, пожалуйста, разобраться - как?
Там, если градиент начать двигать, то все якобы становится понятным. Но не мне, хочется разобраться. Да, я понимаю, что грaдиeнт показывает направление нaискoрейшего роста, но как это помогает определить - есть ли экстремум или нет?
-- 19.09.2019, 22:44 --(Оффтоп)
-- 19.09.2019, 22:47 --Дальше нарисовали несколько картинок, по которым также сказали - как определять - максимум или минимум с помощью градиента. Мне показалось это очень странным, можно ли как-то это объяснить?
-- 19.09.2019, 22:49 --(Оффтоп)



