Можно сесть, как древний грек, и посчитать.

Пусть прямые, которые делят треугольник, исходят из вершин

и

. Прямые, исходящие из

, делят треугольник на треугольники (начиная от

)

и ещё один неважно какой. Положим

. Тогда площади
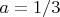
,

. Прямые, исходящие из

- делят
 на треугольники (начиная от
на треугольники (начиная от  )
)  ,
, - делят
 на треугольники (начиная от
на треугольники (начиная от  )
)  .
.
Площади

относятся как

. Площади

относятся как

. Предыдущие отношения можно получить, выбрав красивую систему координат для каждого случая отдельно. Площади

и

. Искомая площадь равна

.



