TL: пока я нашёл только
Wikipedia и
Coxeter. Regular Polytopes,
Regular Complex Polytopes.
Мне интересны: правильные многогранники в пространствах

их группы симметрии, и как они раскладываются, интерпретируются и соотносятся с
группами типа Ли (

...), в частности, диаграммы Коксетера и Коксетера-Дынкина.
----------------
Правильные многогранники Правильные многогранники известны всем: это пять многогранников в трёхмерном пространстве (Platonic solid), а именно, тетраэдр, куб (гексаэдр), октаэдр, додекаэдр, икосаэдр.
Двойственность: у каждого многогранника есть двойственный ему - такой, который получается заменой вершин на грани, а граней на вершины. Например, в центре тяжести каждой грани можно отметить точку, и сделать её вершиной нового многогранника, соединяя их соответственно через рёбра, и так далее. (В действительном случае, можно просто взять выпуклую оболочку получившихся точек, но дальше такая конструкция не обобщается.)
Символ Шлёфли: это обозначение

выражает ту мысль, что "в вершине сходятся

штук

-угольных граней", или что порядок грани

а порядок вершины
 Дальше символ Шлёфли будет определяться по индукции: для
Дальше символ Шлёфли будет определяться по индукции: для  -мерной грани записывается её символ Шлёфли, а в конце дописывается, сколько таких граней сходится в одной вершине в одном элементе коразмерности 3.
-мерной грани записывается её символ Шлёфли, а в конце дописывается, сколько таких граней сходится в одной вершине в одном элементе коразмерности 3. Для двойственного многогранника получается тот же символ Шлёфли, что и для исходного многогранника, но записанный задом наперёд.
Тетраэдр двойственен сам себе (самодвойственен), куб двойственен октаэдру, додекаэдр двойственен икосаэдру.
Vertex figure (линк вершины или вершинная фигура): часто интересна не грань, а окрестность вершины. Наглядно vertex figure можно себе представить как форму среза, если отсечь малую окрестность вершины плоскостью. На языке абстрактных многогранников она определяется иначе: это все грани, инцидентные данной вершине (то есть, содержащие её).
Abstract_polytope#Vertex_figures Но по сути, получается та же фигура. Символ Шлёфли для vertex figure можно найти, если вычеркнуть первую цифру в символе Шлёфли для всего многогранника.
Группа симметрии: она переводит многогранник в себя, то есть является подгруппой движений (изометрий) пространства. Но в других пространствах может не быть изометрий. Поэтому группа симметрии многогранника - это та группа, которая переводит его
флаги в его флаги.
Флаг - это набор из вершины, инцидентного ей ребра, инцидентной им грани, и так далее, до полной размерности

И обратно, это позволяет определить
правильный многогранник: это такой многогранник, группа симметрии которого действует на его флагах
транзитивно, то есть в ней найдётся преобразование, переводящее любой заданный флаг в любой заданный. Группы симметрии двойственных многогранников совпадают, очевидно.
Группы симметрии правильных многогранников - это:
полная группа тетраэдра  - Wiki, Wikiversity, порядка 24;
- Wiki, Wikiversity, порядка 24;
полная группа октаэдра  (она же группа симметрий куба) - Wiki, Wikiversity, порядка 48;
(она же группа симметрий куба) - Wiki, Wikiversity, порядка 48;
полная группа икосаэдра  (она же группа симметрий додекаэдра) - Wiki, порядка 120.
(она же группа симметрий додекаэдра) - Wiki, порядка 120.
Если запретить отражения - несобственные движения - то получаются "просто" (= хиральные) группы тетраэдра

порядка 12, октаэдра

порядка 24, икосаэдра

порядка 60. (Эти обозначения - символы Шёнфлиса (Schönflies), придуманы в 19 веке для кристаллографии, и здесь уже не вполне удобны и логичны, но традиционны. Также есть нотация Коксетера и диаграммы Коксетера.) Эти полные группы порождаются отражениями, и они, и их подгруппы, называются группами Коксетера (
Wiki), в комплексном случае - Shephard group (
Wiki).
Кроме того, есть другие интересные родственные группы:
пиритоэдральная группа  порядка 24,
порядка 24, 
 Wikiversity;
Wikiversity;
бинарные группы  порядков 24, 48, 120, которые являются двойными накрытиями соответствующих хиральных групп, однако не содержат их в качестве подгрупп.
порядков 24, 48, 120, которые являются двойными накрытиями соответствующих хиральных групп, однако не содержат их в качестве подгрупп.  Wiki,
Wiki,  Wiki,
Wiki,  Wiki.
Wiki.
Все эти группы, кроме бинарных, могут быть реализованы как действительные матрицы

а бинарные - как комплексные матрицы

Таким образом, всё это конечные подгруппы в

Кроме того, они изоморфны:
где

и

-
симметрическая и
знакопеременная группы (группы перестановок и чётных перестановок),

-
группа кватернионов (
Wiki).
 Wiki
Wiki,
 Wiki
Wiki.
----------------
В других размерностях В размерности 2 для любого

существует правильный

-угольник, и он самодвойственный. (Традиционно полагается
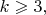
но с абстрактной точки зрения может быть удобно учитывать и

и даже

) Итого, есть бесконечная серия. Символы Шлёфли

Группы симметрий этих многоугольников - (без отражений)

и (с отражениями)

(
Wiki), их двойные накрытия -

(?) и

(
Wiki).
https://en.wikipedia.org/wiki/Regular_polytope(Для разных размерностей есть разные термины: полихоры, политопы и т. д. - я не буду ими пользоваться, пока могу.)
В размерности 4 существует шесть различных многогранников:
из тетраэдров  получается
получается
5-ячейник (симплекс) 
16-ячейник (гипероктаэдр) 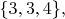
600-ячейник  ;
;
из кубов  получается 8-ячейник (гиперкуб)
получается 8-ячейник (гиперкуб) 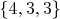 ;
;
из октаэдров  получается 24-ячейник
получается 24-ячейник  ;
;
из додекаэдров  получается 120-ячейник
получается 120-ячейник 
Их двойственности: симплекс двойственен сам себе, гиперкуб - гипероктаэдру, 24-ячейник - сам себе, 120- и 600-ячейники - друг другу. Их группы симметрии:



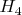
(это уже обозначения Коксетера,
Wiki).
Во всех старших размерностях существует три правильных многогранника:
симплекс  ;
;
гипероктаэдр  ;
;
гиперкуб 
Симплекс двойственен сам себе, гиперкуб - гипероктаэдру. Их группы симметрии:


----------------
В неплоских пространствах (сферическое, эллиптическое, гиперболическое = Лобачевского) возможны другие варианты, или невозможны какие-то из перечисленных.
Некоторые определения обобщаются на звёздчатые многогранники и на регулярные замощения пространства.
Во всё это я залезать не буду.
----------------
В комплексных пространствах  https://en.wikipedia.org/wiki/Complex_polytope
https://en.wikipedia.org/wiki/Complex_polytope В случае комплексного пространства приходится несколько изменить определения. Комплексный многогранник нельзя рассматривать как непрерывную поверхность, как границу области. Вместо этого, каждую грань мы заменяем на плоскость (аффинное подпространство). В
[^] написана какая-то чушь (например, там многогранник может не содержать ни одной вершины), так что лучше взять определение
абстрактного многогранника Wiki, и добавить уже известное условие группы, действующей транзитивно на флагах.
Мир комплексных правильных многогранников богаче. Уже 1-мерные многогранники (в

) образуют бесконечную серию, аналогичную действительным 2-мерным правильным многоугольникам. Дальше:
в размерности 2 - в дополнение к действительным многогранникам, есть две бесконечные серии и 19 исключительных случаев;
в размерности 3 - -"- есть две бесконечные серии и 3 исключительных случая;
в размерности 4 - -"- есть две бесконечные серии и 1 исключительный случай;
в размерности 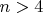 - -"- есть две бесконечные серии.
- -"- есть две бесконечные серии.
Например, в размерности 2 появляются очень интересные дуопризмы и дуопирамиды:
Какие у них группы симметрии? В
не написано о них ни подробностей структуры, ни тем более исключительных изоморфизмов.
----------------
Над конечными полями? Определения, модифицированные для

легко (почти автоматически) переносятся на
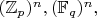
но в Wikipedia про это ни слова. Известны ли правильные многогранники хотя бы в

? (Я специально упоминаю побольше, потому что в совсем малых характеристиках могут возникнуть новые трудности.) Какие у них группы симметрии?



