Не могли бы подсказать, в каком месте рассуждения (чуть выше) логика не правильная?
Например откуда вы взяли вторую систему? — туда должны входить не

, а элементы обратной

матрицы.
-- Вт сен 03, 2019 21:43:56 --Тут есть одна неприятная проблема в терминологии (насколько я в курсе; хотя если читать только какую-то одну книгу, этого будет не видно) в том, что сопряжённым и/или транспонированным отображением называют иногда две разные вещи.
Первая определена для любого линейного отображения
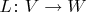
, обозначим её

и определяется она как
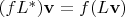
, где

произвольные; более аккуратно это будет
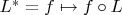
(но так труднее видеть естественность?..).
Вторая определена только для таких отображений

, что

имеют какие-то (невырожденные) билинейные формы

(обычно скалярное произведение или эрмитово скалярное произведение). Тогда можно определить
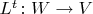
таким образом:

, где
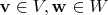
произвольные. Можно определить
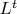
через

и билинейные формы.
Вторая штука делает из матрицы транспонированную, используя канонические скалярные произведения на пространствах

-элементных столбцов, столбцам

сопоставляющие

. Первая штука оставляет матрицу как есть, мы просто умножаем её не на столбец, а на строку. С учётом того, что матрица линейного отображения определена для любого отображения

, будь только выбраны базисы в

, нам не обязательно интересоваться транспонированными матрицами, пока мы не начнём говорить о каких-нибудь евклидовых или гильбертовых

. Когда начнём, тогда сможем например умножать матрицу на транспонированную к ней с осмысленным результатом.