ewert, спасибо за ответ.
Если в книжке буквально так, то это неправильная последовательность
Да,
Axler дословно пишет при определении комплексных чисел:
Axler писал(а):
A complex number is an ordered pair

where

,


, but we will write this as

.
И лишь затем определяет сложение и умножение.
Но я параллельно еще читаю
Привалов, Введение в теорию функций комплексного переменного и там идёт изложение в таком порядке, как Вы и написали.
И тогда, определив умножение и сложение можно доказать что при определенных таких образом операциях

можно записать как

.

.
Но тут ещё возникает вопрос.
Потом отождествить пары определённого вида с вещественными числами -- и, конечно, доказать, что это соответствие есть изоморфизм.
Это делается таким образом?
1.Введём отображение

.
2.Докажем, что это отображение сохраняет операции сложения и умножения.

.
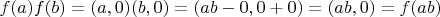
.
Таким образом, действия на образах согласуются с действиями на прообразах (арифметическими действиями над вещественными числами). То есть рассматривая множество вещественных чисел как подмножество комплексных чисел, мы можем оперировать над ними таким же образом, как оперировали до введения нового поля.
Это верно?
Привалов говорит об этом, но не оперирует понятием "изоморфизм" (относительно полей я также не знал что это) и не вводит явно отображение, говорят, что "условимся обозначать".
-- 09.09.2019, 20:31 --beroal, спасибо за ответ.
До "не наивной" теории множеств я доберусь только после того как почувствую что владею стандартным материалом на достаточном уровне. Но да, уже иногда возникает желание хотя бы в Википедии посмотреть, как же там строится эта пресловутая

, что там не возникает таких вопросов.
Если доказывать, что операции на комплексных числах удовлетворяют аксиомам поля, кажется нудным, тогда есть другой путь — факторкольцо
![$\mathbb{R}[X]/I$ $\mathbb{R}[X]/I$](https://dxdy-03.korotkov.co.uk/f/6/8/0/6804dea1b94a6db2946d0b45ca97f6df82.png)
, где идеал

порождён многочленом, который легко угадать.
Видел такое (если я правильно усвоил обозначения) у
Terence Tao, вот тут -
https://terrytao.wordpress.com/2016/09/ ... x-numbers/ , но почувствовал, что это куда более сложная теория, и хоть этот подход и "общий" для таких дел, придется его тоже отложить.



