Recall the Vector Field Straightening Theorem.
If at a point
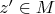
the Hamiltonian is non-degenerate:
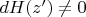
then in some open neighborhood

of the point
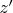
there exist a local symplectic coordinates
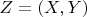
such that
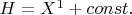
Observe also that since
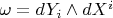
and
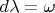
then in these new coordinates one has

Suppose that the curve
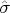
has its ends at points
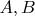
and we have already parametrized an arc of the curve from the point

to a point
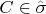
by means of parametrization
![$$\hat z(t),\quad \hat z(t_A)=A,\quad \hat z(t_C)=C,\quad t\in[t_A,t_C]$$ $$\hat z(t),\quad \hat z(t_A)=A,\quad \hat z(t_C)=C,\quad t\in[t_A,t_C]$$](https://dxdy-03.korotkov.co.uk/f/e/6/f/e6f3a8f8333300e3fabba906211516d982.png)
and
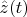
is a solution to system (*). The point

is situated between the points
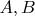
at the curve.
Introduce the coordinates

in some open neighborhood

of the point

.
The manifold
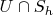
is determined as follows
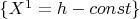
. So that
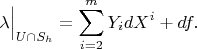
Let
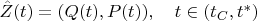
be a parametrization of
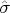
from the point

to some other point at the exit from

.
Consider the following perturbation
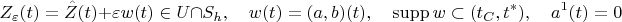
of the curve
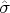
. This perturbation is denoted by

.
So that after integration by parts we get
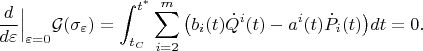
This implies that the functions
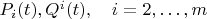
are identical constants.
We also have
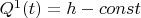
. The variable
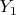
is changed freely along the curve
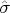
. Consequently if
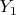
-coordinate of the point

is equal to
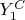
then we can put
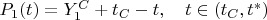
.
It is easy to see that the vector
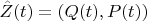
satisfies system (*) for
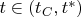
. The function
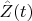
is continuous at the point
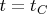
. Moreover,
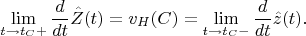
Then we straight the vector field

in a neighborhood of the point
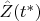
and so on.



