nnosipovДоказательство от 19.08 всё же не бесполезное. Напомню
Вернемся к уравнению

и будем исходить из из предположения, что любой остаток вида

, не превышающий по абсолютной величине

соответствует если не подходящей, то хотя бы промежуточной дроби разложения

(

вз. просты). Вроде бы это верно для любых разложений, но могу ошибаться. Требуемое разложение можно записать в общем виде:

Тут выписаны три подходящие дроби, включая нулевую. Этого достаточно, поскольку период из двух знаков. Выпишем соответствующие остатки:



Нужного остатка

в этом списке нет, значит переходим к промежуточным дробям. Возьмем первым знаком не

, а некоторое

, тогда первой дробью будет

. Запишем уравнение

. Получаем

(то, чего хотелось избежать). Второй знак можно не проверять, поскольку там будут положительные остатки, а вот в третьем знаке имеем

вариантов. Тут нужно воспользоваться формулой рекуррентной зависимости для квадратичных вычетов

. Подставляя в нее

, получаем уравнение

или

Отсюда

и опять же

Если нет ошибки в допущении, это доказательство.
Возьмем теперь произвольные

, рациональное

и вычислим

. Если к этой дроби добавить слева палиндром с нулем

, то для новой дроби

также будет выполняться

Обозначим третий остаток новой дроби буквой

, тогда разложение

можно еще выразить так:

. Таким образом, если в вышеприведенном доказательстве заменить целое

на рациональное, необходимость в допущениях отпадает. Положим

. Выражение

меняется тогда на

, и видно что

всё-таки целый квадрат без единицы. Неполнота этого доказательства в том, что пара

(решение изначального уравнения) предполагается вз. простой, а этого в условии не сказано. Более того, из предположения

уже следует

. Поясню. Перепишем систему

так:

и перемножим почленно:

, или

. Пара

может иметь общий делитель

, а вот откуда следует вз. простота

мне не очень понятно. Дальнейшие сокращения приводят к уравнению
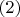
, которое тоже не приносит облегчения. Остается либо доказать что

вз. просты, либо (как альтернатива) заменить из доказательства выше уравнение

на

, допустив рациональное

и

. Тогда числитель и знаменатель дроби

, домноженные на

дают решение. Если уравнение разрешимо.