Дайте, к примеру, вашу интерпретацию функции распределения непрерывной случайной величины.
Доля площади под кривой соответствующей функции плотности распределения.
-- 19.08.2019, 18:14 --А как бы вы тогда назвали обратное отношение (которое всегда
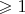
?
А разве в общепринятой теории вероятности как-то специально рассматривается величина, обратная вероятности?
-- 19.08.2019, 18:29 ---_-Вспомните условную вероятность

— это обычная вероятность

в «вероятностном подпространстве»…
Заодно видно, когда будут проблемы: если мера какого-то множества бесконечна или ноль, вы не сможете такой конструкцией получить вероятностное пространство (нельзя получить нормированную меру).
Возможно, я чего-то недопонимаю; собственно, я и открыл эту тему в надежде на то, чтобы разобраться, чего именно. Но я не вижу, в чём разница моей интерпретации для условной вероятности по сравнению с «безусловной». Вы сами пишете, что условная вероятность — это то же самое, что просто вероятность, но в другом вероятностном пространстве.
С бесконечной или нулевой мерой я тоже пока не разглядел проблем. Я был бы вам признателен за конкретный пример типа такого: в таком-то конкретном случае общепринятая теория вероятности говорит, что такая-то вероятность равна
X, но в моей интерпретации через «долю меры» для этого случая нельзя указать таких множеств
a и
A и такой меры, чтобы доля меры
a от меры его надмножества
A составляла именно
X.