Об измеримости интегралов специального вида

[Evgenii2012]

Уважаемые коллеги есть два принципиально важных вопроса, которые я очень хотел бы обсудить с Вами.

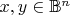
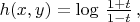
Прежде всего, приведу определения, необходимые для их формулировки. 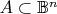Определим гиперболическое расстояние между точками $x, y\in {\Bbb B}^n$ единичного шара ${\Bbb B}^n:=\{x\in {\Bbb R}^n: |x|<1\}$ согласно соотношению $h(x, y)=\log\,\frac{1+t}{1-t}\,,$ где $t=\frac{|x-y|}{\sqrt{|x-y|^2+(1-|x|^2)(1-|y|^2)}}\,.$ Теперь, введём гиперболическую $n-1$-мерную хаусдорфову меру $\mathcal{H}^{n-1}_{h}(A)$ множества $A\subset {\Bbb B}^n$ согласно формул:

$$\mathcal{H}^{n-1}_{h}(A):=\sup_{\varepsilon>0}\mathcal{H}^{n-1}_{h,\varepsilon}\,,$$

где

$$\mathcal{H}^{n-1}_{h,\,\varepsilon}(A):= \Omega_{n-1}2^{\,-{(n-1)}} \inf\sum^{\infty}_{i=1}\left(h(A_i)\right)^{n-1},$$

$\Omega_{n-1}$ -- $(n-1)$-мерная лебегова мера единичного шара ${\Bbb B}^{n-1}$ в ${\Bbb R}^{n-1}.$
Пусть $Q$ -- неотрицательная измеримая в ${\Bbb B}^n$ функция относительно обычной лебеговой меры. Для $0<r<\infty$ обозначим $S_h(0, r)$ гиперболическую сферу с центром в нуле радиуса $r$ т.е., $S_h(0, r)=\{x\in {\Bbb B}^n: h(x, 0)=r\}.$ Пусть $\psi(r)=\int\limits_{S_h(0, r)}Q(x)d\mathcal{H}^{n-1}_{h}.$
(При заданном условии на $Q$ её измеримость относительно $\mathcal{H}^{n-1}_{h}$ сравнительно легко доказать. Хорошо известно, что замкнутые множества измеримы относительно любых Хаусдоровых мер, так что $S_h(0, r)$ измеримо относительно $\mathcal{H}^{n-1}_{h}$).

Вопрос 1. Будет ли функция $\psi(r)$ измерима по $r\in (0, \infty)$ ?

Вопрос 2. Верен ли "гиперболический" вариант теоремы Фубини:

$$\int\limits_{B_h(0, r_0)}Q(x)dv(x)=\int\limits_{0}^{r_0}\int\limits_{S_h(0, r)}Q(x)\mathcal{H}^{n-1}_{h}dr,$$

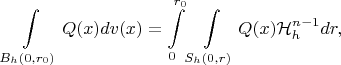
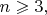
где $0<r_0<\infty$ и $dv(x)=\frac{2^n\, dm(x)}{{(1-|x|^2)}^n},$ $dm(x)$ -- элемент обычной лебеговой меры. Меня, прежде всего, интересует случай $n\geqslant 3,$ так как при $n=2$ это относительно простые и известные вещи.

Также хотел бы уточнить, не видел ли кто-либо в литературе (интернете) выражение элемента площади $\mathcal{H}^{n-1}_{h}$ в терминах обычной, евклидовой меры $\mathcal{H}^{n-1}$ (подобно тому, как для гиперболического объёма, как написано выше, $dv(x)=\frac{2^n\, dm(x)}{{(1-|x|^2)}^n}$) ?

Буду очень благодарен Вам за любые комментарии !

[Brukvalub]

Evgenii2012 в сообщении #1410904 писал(а):

Теперь, введём гиперболическую $n-1$-мерную хаусдорфову меру $\mathcal{H}^{n-1}_{h}(A)$ множества $A\subset {\Bbb B}^n$ согласно формул:

$$\mathcal{H}^{n-1}_{h}(A):=\sup_{\varepsilon>0}\mathcal{H}^{n-1}_{h,\varepsilon}\,,$$

где

$$\mathcal{H}^{n-1}_{h,\,\varepsilon}(A):= \Omega_{n-1}2^{\,-{(n-1)}} \inf\sum^{\infty}_{i=1}\left(h(A_i)\right)^{n-1},$$

Какое-то "криво-сделанное" определение меры. Нет описаний некоторых используемых в этом определении объектов.

[vpb]

Да, в этом определении явно не хватает каких-то слов и объяснений. Например, что такое $A_i$ и $h(A_i)$.

[DeBill]

vpb в сообщении #1410933 писал(а):

такое $A_i$ и $h(A_i)$.

Ну, если ТС работает с хаусдорфовой мерой, то , видимо, рассматриваются произвольные покрытия измеряемого множества шарами радиусов $A_i <\varepsilon $....
И -так кажется - мера у ТС получится какя то стандартная совсем, типа, индуцированная гиперболической метрикой....

(Оффтоп)

Проверять, видимо, можно по такому плану: убедиться в правде для шариков с центром в нуле, и сослаться на инвариантность мер относительно соответствующей гиперболической группы (буде таковая есть).

[Evgenii2012]

Дорогие друзья, большое спасибо за Ваши замечания. Действительно, я должен кое-что уточнить: $A\subset \bigcup\limits_{i=1}^{\infty} A_i,$ где $A_i$ -- множества, имеющие гиперболический диаметр $h(A_i):=\sup\limits_{x, y\in A_i}h(x, y),$ меньший $\varepsilon.$ Согласно, например, [Hurewicz W., Wallman H.: Dimension Theory. Princeton Univ. Press, Princeton, NJ (1948)], глава VII, страница 103, либо [Martio O., Ryazanov V., Srebro U. and Yakubov
E. Moduli in Modern Mapping Theory. -- New York: Springer Science + Business Media, LLC, 2009], страница 177, множества $A_i$ открытыми быть не обязаны (!), что, впрочем, вероятно, принципиальным не является