ИМХО, строго говоря, неверно. Ваша запись соответствует более сильному утверждению, из которого, в частности, следует аксиома 2
Да, я как-то подзабыл про независимость аксиом друг от друга. Тем не менее, аксиома 2 из моей записи аксиомы 4 не следует. Из неё следует, что если мы возьмём три коллинеарные точки, то одна из них (скажем, С) будет лежать как между А и В, так и между В и А. Это тоже плохо, так как из словесной формулировки подобное заключение вывести нельзя, но формально эта запись не отменяет того случая, когда для каких-нибудь трёх неколлинеарных точек

, а
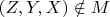
.
Я не читал Расина, но в оригинале у Гильберта другие аксиомы.
Идейно они близки. Цитата из книги: "В первой главе на основе системы аксиом, близкой к системе аксиом Д.Гильберта (см. [2]), строится достаточно представительный "кусок"планиметрии." Всё-таки книгу, написанную для современных мат. школьников, поприятнее читать, чем перевод 1920-х годов.



