1. Можно ли полагать, что такой странный график получается из-за неточности вычислений?
2. И, если это не точный график, то можно ли нарисовать точный?
3. Есть ли способы исследования этой функции?
1. Да. Именно поэтому. В числителе у Вас сумма единицы с очень малым числом. Когда оно становится сравнимо по порядку с младшими разрядами при заданной точности (7-8 при одинарной, 13-14 при двойной и т.п.), разряды, не представимые в данной точности, теряются, и Вы имеет дело с игрой ошибок округления.
2. Можно. Руками. Имея в виду, что это у Вас приближения ко "второму замечательному пределу", так что будет приближаться к
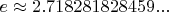
, так что будет плавное приближение к данному числу. Ну, или можно поиграть с числами повышенной точности, но это из серии "не беги от медведя, умрёшь уставший", эффект останется, но будет проявляться при больших значениях аргумента. Хотя чисто в педагогических соображениях попробовать можно, или даже оформить, как доклад на студенческой конференции "влияние точности вычислений".
3. Ну, есть приёмы, с которыми в школе знакомили (в кружках больше). Асимптоты, максимумы, пересечения нуля... Институт добавит про производные.



