Составное число первого порядка — это составное число, уменьшив которое на некоторый его собственный (отличный от 1 и самого числа) натуральный делитель, можно получить простое число.
Составное число второго порядка — это составное число, уменьшив которое на некоторый его собственный (отличный от 1 и самого числа) натуральный делитель, можно получить составное число первого порядка, но получить простое число вышеописанным способом нельзя.
Составное число порядка

— это составное число, уменьшив которое на некоторый его собственный (отличный от 1 и самого числа) натуральный делитель, можно получить составное число порядка

, но получить число более низкого порядка вышеописанным способом нельзя.
---
А теперь собственно вопрос. Можно ли найти формулу, определяющую порядок составного числа? Например, любое число вида

, где
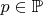
(то есть любое удвоенное простое число), является составным числом первого порядка, так как уменьшив его на

мы

же и получаем.
А дальше уже сложнее. Например, несколько первых составных чисел второго порядка выглядят следующим образом: 8, 9, 12, 15, 16, и некоей общей закономерности тут пока не просматривается (во всяком случае, автор данных строк пока её не видит).
А вот первым составным числом третьего порядка является уже 18, и тоже непонятно, по какой причине.
---
В общем, пожалуйста, помогите разобраться.



