Ведь если у нас есть множество функций, непрерывных в интервале ("б"), то в этом множестве можно выделить множество функций, непрерывных в некоторой внутренной точке этого интервала ("а").
Нет, ровно наоборот. Если функция непрерывна на интервале
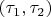
("б"), то это означает, что она непрерывна на каждой точке этого интервала. То есть, она непрерывна и в заданной точке

То есть, любая функция из множества "б" безусловно попадает и во множество "а". А обратное неверно: функция, непрерывная в

может не быть непрерывной в какой-то точке

Такая функция тоже попадёт в "а", но не попадёт в "б".
-- 27.07.2019 15:20:10 --Вот у нас три множества:
к) множество всех котов;
л) множество всех котов, у которых правая передняя лапа - белая;
м) множество всех котов, у которых все лапы белые.
Расставьте знаки включения между этими множествами.
-- 27.07.2019 15:21:42 --Против вашей интуиции может быть то, что накладывая
больше условий, мы получаем
меньшее множество. Но это просто так, к этому надо привыкнуть.



