Не могли бы вы вспомнить формулировку задачи с олимпиады?
Пусть

--- натуральное число. Докажите, что, если число
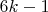
составное, то

можно представить в виде
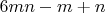
с натуральными

и

.
Это несложная задача.
Интересно

А если составное

, то

должно быть представимо в виде

или

Хотя.. эти два выражения эквивалентны относительно одновременной замены знаков у

и

как-то незаконченный разговор..
Задача интересная, но простая она тогда, когда уже знаешь ответ )))
Делителями любого числа виде
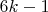
должны быть одновременно числа двух видов -

и число вида

. Перемножаем и получаем
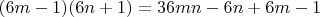
. Что соответствует

Для чисел вида

делителями могут быть или одновременно

и

, или

и




