Я так понимаю, что вопрос состоит в том, как понимать вольную фразу из Халмоша о том, что одна мера способна быть отличной от нуля лишь там, где другая равна нулю. Там не даром стоит слово "вообще" :) Приведу пример, который мне ближе. Вместо зарядов я буду рассматривать неотрицательные меры, к тому же нормированные (т.е. вероятностные). Пусть мера

есть любое абсолютно непрерывное (по мере Лебега) распределение - например, нормальное

где
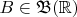
есть любое борелевское множество. Пусть мера

есть любое дискретное распределение (для определённости, на множестве целых чисел) - например, распределение Пуассона

Легко видеть, что это взаимно сингулярные меры: пусть
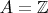
,

. Тогда

,
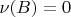
, ну и

,

для любого борелевского

.
Грубо говоря, "носители" этих мер не пересекаются - мера

сосредоточена на множестве целых чисел

, мера

- на множестве

, т.е. на числовой прямой с выколотыми целыми точками. Именно это и имелось в виду той самой фразой из Халмоша: что множества, на которых положительна одна мера, есть нулевые множества другой, и наоборот. Попытка придать этой фразе точный смысл просто продублирует определение: если множество

таково, что

, то и
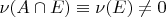
- мера ничего не потеряет от сужения на множество

. Но

. И наоборот.
А высказывание

, конечно же, неверно. Достаточно здесь взять

(ну или всё

).



