Доказывается утверждение, что если

дифференцируема на

, то

непрерывна в любой точке
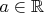
и спрашивается, где в приведенном доказательстве ошибка
Доказательство
По теореме Лагранжа

, где

- точка между

и

. Тогда если

, то

. По определению

, и поскольку этот предел существует, то существует и равен ему предел правой части формулы Лагранжа, то есть

при

. Непрерывность

в точке

"доказана".
Мне кажется, что ошибочно утверждение, что

. Для того, чтобы определить, существует ли предел в правой части надо рассматривать окрестности точки

и роль играют значения функции

во всех точках окрестности. Теорема Лагранжа утверждает, что что существует точка

, лежащая между

и

, такая что

и ничего не говорит о значении

в других точках окрестности.
Прав ли я?



