Вот Вам для развлечения совершенно реальная задача из жизни. (Ко мне в разное время с этим вот вопросом обращались два разных человека, занимающихся изготовлением дверей). Требуется изготовить дверь в форме прямоугольника, завершённого круговым сегментом, как на рисунке:
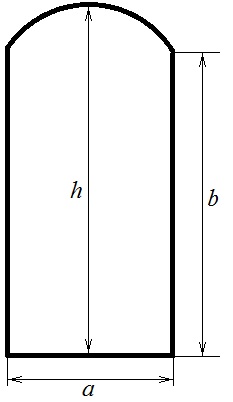
Известны размеры прямоугольной части дверного полотна, а также высота двери по оси симметрии. Каков должен быть радиус кривизны верхнего сегмента? (У плотника есть инструменты, позволяющие ему делать как прямолинейные распилы, так и распилы вдоль дуги окружности, но чтобы не переводить материал зря, нужно сразу точно вычислить радиус этой дуги). Задачу требуется решить в общем виде, то есть, предоставить плотнику готовую формулу, по которой он в дальнейшем сам сможет найти этот радиус при любых значениях

. У плотника есть калькулятор, позволяющий выполнять четыре действия арифметики, а также извлекать квадратные корни. Но тригонометрия для него - тёмный лес. Поэтому, на всякий случай: формул с тригонометрическими функциями предлагать нельзя.



