Используя аксиому непрерывности меры для убывающей последовательности множеств
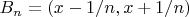
, доказать, что мера Лебега одноточечного подмножества

вещественной прямой равна нулю:

. Используя этот факт, доказать, что
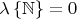
,

,

,
![$\lambda(a,b)=\lambda[a,b]$ $\lambda(a,b)=\lambda[a,b]$](https://dxdy-04.korotkov.co.uk/f/3/e/9/3e9ef46b5cf9721c12b73fdfebb29bf282.png)
.
C мерой я особо управляться еще не научился, поэтому прошу проверить мои элементарные выкладки.
Аксиома непрерывности:
Дана убывающая последовательность

множеств из сигма-алгебры
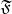
, причем

. Пусть
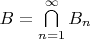
Тогда
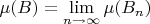
.
В нашем случае
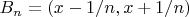
и

.
По аксиоме непрерывности

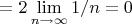
.
В третьем равенстве использовалась теорема о том, что величина меры Лебега интервала на прямой равна его длине.
Множества
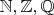
-- счетные, поэтому их можно представить в виде счетного объединения одноточечных подмножеств. Воспользовавшись сигма-аддитивностью меры получим счетную сумму нулей в качестве меры этих множеств.
Таким же образом закрытый интервал можно представить в виде объединения открытого интервала с двумя одноточечными подмножествами -- концами этого интервала, мера Лебега которых равна нулю.



