Читаю лекции Гельфанда по линейной алгебре. Цитата из лекции:
Цитата:
Таким образом,
если векторы  линейно зависимы, то хотя бы один из них является линейной комбинацией остальных
линейно зависимы, то хотя бы один из них является линейной комбинацией остальных. Мы предоставляем читателю проверить, что верно и обратное, т. е., что
векторы, один из которых есть линейная комбинация остальных, линейно зависимы.
Не могли бы вы проверить мою проверку (см. ниже) последнего утверждения?
Проверка. Пусть

— некоторое линейное пространство. В

заданы множество векторов

и множество скаляров

. Пусть также вектор
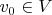
есть линейная комбинация некоторых векторов множества

:

Тогда очевидно, что существует неравный нулю скаляр

такой, что

существует такой скаляр

такой, что
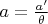
:

Следовательно, мы получили линейно зависимые векторы

, так как, как минимум, скаляр

не равен нулю.
P. S. И еще, правильно ли я понимаю, что термины «линейное пространство», «афинное пространство» и «векторное пространство» эквиваленты? Если так, то какова этимология названий линейного и афинного пространств (с векторным все очевидно)? На счет «линейного» есть догадка, что оно так называется, потому что пространство определяется множеством, полем и двумя
линейными операциями: сложением и умножением на скаляр. Но, опять же, почему эти операции называются линейными?



