т.е. в такой формулировке доказывается, что множество бесконечных комбинаций цифр 0-9 несчетно?
Нет. Множество всех бесконечных последовательностей <из> десяти цифр действительно несчётно. И это можно доказать, используя диагональный метод. Но вы рассматриваете все бесконечные последовательности с
конечным числом ненулевых цифр. Это множество счётно.
Ошибка в применении диагонального метода состоит в том, что вашим способом нельзя построить последовательность с конечным числом ненулевых цифр. Разве что из подмножества натуральных чисел.
Ни при какой нумерации нельзя так расставить все натуральные числа в вашей таблице, что на диагонали будет стоять лишь конечное число нулей. Это как раз следует из того, что множество всех натуральных чисел всё-таки счётно.
Приснилось бытовое объяснение. Вы думаете, что существует некоторый перечень всех натуральных чисел, который с помощью таблицы, а конкретно диагонали, даст натуральное число, отличающееся от всех чисел из перечня, то есть в него не входящее. Для этого диагональ должна содержать конечное число нулей, чтобы в искомом числе появилось конечное число ненулевых цифр. Но при
любом перечне однозначные числа принесут в диагональ не менее

нулей, двузначные не менее
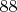
нулей, трёхзначные не менее
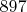
и так далее. То есть чисто интуитивно видно, что в диагонали всегда будет бесконечное число нулей, в соответствующей последовательности — бесконечное число ненулевых цифр, и она не может представлять натуральное число.



