Я честно, что-то все равно не понял.
Можно я приведу свое решение.
Согласно условию у нас пять уровней

1. Скажем у нас пять ячеек соответствующих 5 уровням. 1-я ячейка -1 уровень, 2-я - 2 уровень, ..., 5-я - 5 уровень.
2. у нас 9 интервалов, т.е.

куда можно положить ступеньку

3. возьмем размещение без повторения 9 интервалов, т.е. чисел от 1 до 9 по 5 ячейкам уровней, что равно

4. так как размещение без повторения означает 5 разных чисел, а числа линейно упорядочены, то на
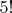
перестановок приходится одна линейная упорядоченность чисел.
5. теперь рассмотрим линейно упорядоченные числа по ячейка

. Интервал 2 в ячейке 1-ой, 4 - в 2-ой, 6 - в 3-ей, 7 - в 4-ой и 8 - в 5-ой ячейке.
6. интервал 2 уровня 1-го и все числа меньше него, т.е интервал 1 тоже 1-го уровня, так как в ячейке первой; ступенька на интервале 4 - уровая 2-го и все интервалы до интервала 2, т.е интервал 3 - 2-го уровня и так далее, а интервал 8 на 5 уровне и все интервалы после него т.е. интервал 9 тоже 5 уровня.
7. у меня получается

Правильны ли мои рассуждения и правильный ли расчет из рассуждений ?



