Как из этого следует, что

тоже является функцией, которая возвращает

-ю координату?
Во-первых, надо понимать, что

не "тоже".
 - это функция, возвращающая
- это функция, возвращающая  -ю координату аргумента
-ю координату аргумента 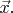
 - это функция, возвращающая
- это функция, возвращающая  -ю координату другого аргумента
-ю координату другого аргумента  хотя от
хотя от  она тоже зависит.
она тоже зависит.
Во-вторых, как следует.
Строго применением формулы

А именно, когда нам дана функция
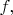
то чтобы найти

(это можно читать как

то есть оператор

применённый к

), нам надо взять полный набор частных производных этой

по всем координатам
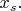
(Тут есть тонкость. Выше я сказал, что координата - это функция. Но чтобы взять частную производную по координате, надо иметь в виду не только одну эту координату, но и всю остальную
систему координат, в которую данная координата входит.)
Например, разберём нашу плоскость
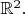
На ней заданы координаты

(Я не одобряю предложения Slav-27 поменять обозначения, поскольку это вас запутает: пока у вас есть ваши базовые обозначения по лекциям или учебнику, и вы к ним привыкаете, лучше их придерживаться. Я только вместо черты пишу вектор, потому что черта - это всего лишь упрощённый способ написать значок вектора.)
Рассмотрим функцию

Понятно, как она себя ведёт: в точке

она равна

а в точке

она возвращает
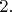
Возьмём набор её частных производных:
Тут всё понятно?
И наконец, запишем
Мы получили функцию от аргументов

каждый из которых - два числа. И она возвращает 1-е число из аргумента
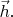
Игнорируя все остальные аргументы (в данном случае; такую простую систему координат мы выбрали).
Убедитесь, что
 -- 06.06.2019 16:51:35 --
-- 06.06.2019 16:51:35 --
-- это функция, определённая на множестве

и принимающая значения в множестве линейных функций из

в

Это можно написать и так:

.
Может быть, стоит "по-программистски"?

Если это поможет понять.
И ("декаррирование") это то же самое, что




