1. Ареа-функции - это устаревшее обозначение арк-функций?
Нет, это подчёркивает различие геометрического смысла обратных функций:

- "дуга"

- "площадь"
Общее правило такое: с тригонометрическими функциями приставка

с гиперболическими - приставка
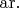
Также упоминается, что некоторые авторы используют приставку

"аргумент".
Применительно к гиперболическим функциям в беглой речи часто употребляют "арк-", и даже пишут в западных обозначениях



но все понимают, что это ошибка. Это позволительно только в таких неформальных жаргонных ситуациях, когда слушатели понимают говорящего, примерно на таком же уровне, на котором употребляются словечки типа
"шинус", "кошинус" или "чосинус", "тхангенс" или "θангенс" и т. п.
Начинающему математику важно обратить внимание на другую важную деталь: иногда обратные функции пишут с большой буквы, а иногда с маленькой. Смысл этого различия в том, чтобы сказать, что используется многозначная комплексная функция, или только одно её главное значение. Но когда что - это в разных источниках по-разному, и надо уточнять.
2. В параметрических уравнениях различных кривых или поверхностей параметр

- это всегда площадь или объём чего-либо (сектора и т.п.)?
Ни в коем случае. Параметр может быть чем угодно.
3. Я никак не могу понять, для чего нужны гиперболические функции. Написано, что используются в различных научных дисциплинах, но какое они дают преимущество, мне пока не ясно
А тогда зачем вы вообще за них взялись?!?
Они нужны там, где возникают. Например, при решении дифференциальных уравнений в одной ситуации возникают тригонометрические функции, а в другой очень похожей ситуации - гиперболические. И чтобы ещё больше подчеркнуть сходство этих ситуаций, записывают похожие формулы.
А если вы пока не столкнулись с областью математики, в которой нужны эти функции, то и забудьте про них!