Приобрёл книжечку Троицкого по аналитической геометрии, чтобы на досуге изучать геометрию. Дошел до теоремы про коническую поверхность над эллипсом.
(Теорема): Коническая поверхность над эллипсом - конус 2-ого порядка.
Доказательство:
Выберем такую систему координат в пространстве с центром в точке, что плоскость

имеет уравнение

. Если мы выберем направления осей

и

параллельно главным осям эллипса, то уравнение эллипса в плоскости

(плоскости эллипса) примет вид:

, где

. Тогда уравнение конической поверхности над ним:

. Действительно, точка (x,y,z),

, принадлежит поверхности тогда и только тогда, когда точка

принадлежит кривой, т.е.

. Но при сделанном предположении

данное уравнение равносильно выводимому. Осталось доказать, что при

выводимое уравнение определено и его множество решений совпадает с О. Определённость следует из того, что во втором сомножителе степень

равна 2 и при умножении пропадает. После умножения уравнение превращается ( при

) в

. Поскольку ассимтотических направлений у эллипса нет, то

?
Итак,

.
После замены
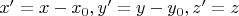

, т. е. конус.
Честно говоря, я не очень понял это доказательство. В связи с этим у к вам, дорогим математикам, несколько вопросов:
1) Почему коническая поверхность имеет именно уравнение

? Я не знаю, может быть, этот вопрос уровня 1 класса, но до сих пор не могу понять, откуда его взяли. Рисовал рисунки, но так не до конца и не понял.
2) Почему там стоит
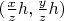
в аргументах функции

?
Если брать

и

при различных

из различных сечений, параллельных плоскости

, то аргументы как раз должны быть

(из подобия треугольников).



