тут еще некоторая проблема с "растворением". Не пойму как это сделать алгебраически. Некоторые идеи, конечно, есть, но они какие-то не завершенные. В общем, провел такое наблюдение:
Допустим есть два числа
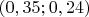
. Очевидно, чтобы растворить второе в первом нужно сложить

. Вопрос: Как из

получить

. Задумался и не знаю как, но размышления вывели меня на такой алгоритм:
1)

2)

3)

4)
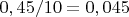
5)

Для второго числа все почти то же самое, но добавляется еще одно деление на 10:
1)

2)

3)

4)

5)
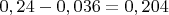
6)

Попытался обосновать это свое наблюдение для более общего случая - вот что получилось:

или:

А дальше у меня 2 тупика:
1) Пока что это подходит только для случая с числами, имеющими только два знака после запятой. Для более общего вида у меня нет алгоритма
2) Задавшись числом (пусть даже и с двумя знаками после запятой), я не знаю как алгебраически получить для него




