Всё очень просто. Да, есть два способа перемножать перестановки. А именно, если у вас записано

то её можно воспринимать:
- слева направо: сначала вычисляется перестановка

а потом к её результату применяется перестановка
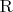
;
- справа налево: сначала вычисляется перестановка

а потом к её результату применяется перестановка

Оба варианта "законны": первый естественный для "наивного" читателя, и если перестановки воспринимать просто "как объект в себе",
а второй - естественный, если воспринимать перестановки как (биективные) функции, а умножение - как композицию:

Так что вся проблема сводится к тому, что где-то в начале раздела про перестановки в книге просто указывается, в каком именно смысле здесь понимается порядок умножения. Надо это место внимательно прочитать, и запомнить. Выкладки одного типа переводятся в выкладки другого типа автоматически: просто записываются задом наперёд. Соответственно, и сопоставить две книги не проблема.



