| Заслуженный участник |
 |
30/01/06
72407
|
Школьная геометрия ( евклидова геометрия на плоскости и в 3-мерном пространстве) устроена так: 1. Создаём пространство точек. Это очень просто: у нас есть действительные числа  и операция декартова произведения множеств. Множество  обычно обозначаемое 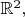 состоит из всех упорядоченных пар действительных чисел, множество  - из упорядоченных троек, и вообще,  - из упорядоченных  -ок (читается "энок"; по-английски  - tuple (en-tuple)). Таким способом можно создать 0-мерное пространство (одна точка), 1-мерное (прямая), 4-мерное, и так далее. 2. Снабжаем это пространство разными структурами. 2.1. Топологическая структура указывает, какие точки считать близкими, а какие - нет, чтобы можно было брать пределы последовательностей и сходящихся окрестностей. Топологическую структуру на  можно взять самую простую: вокруг каждой точки можно взять самую простую: вокруг каждой точки  мы можем обвести параллелепипед, состоящий из произведения отрезков мы можем обвести параллелепипед, состоящий из произведения отрезков  содержащих содержащих  -тую координату точки: -тую координату точки:  Отрезки берутся открытые, потому что в топологии больше любят открытые множества. И дальше все такие параллелепипеды называются базой окрестностей данной точки. Это не все окрестности, но все можно получить из окрестностей базы. В том числе, получающаяся топология не будет зависеть от того, как мы изначально проводили оси координат в нашем пространстве. Но всё это доказывают в продвинутых курсах. Отрезки берутся открытые, потому что в топологии больше любят открытые множества. И дальше все такие параллелепипеды называются базой окрестностей данной точки. Это не все окрестности, но все можно получить из окрестностей базы. В том числе, получающаяся топология не будет зависеть от того, как мы изначально проводили оси координат в нашем пространстве. Но всё это доказывают в продвинутых курсах.
2.2. Линейная структура указывает, какие линии считать прямыми, а какие - нет. Кроме того, на каждой прямой, как на числовой прямой, вводится порядок точек и сравнение длин отрезков. Эти структуры на двух параллельных линиях однозначно связаны (потому что их можно перенести другими линиями, завершающими параллелограмм). В 3-мерном пространстве вводятся плоскости, и на каждой плоскости - линейная структура прямых; на двух параллельных плоскостях структуры связаны. И дальше по индукции, на  -мерном пространстве вводятся -мерном пространстве вводятся  -мерные гиперплоскости, каждая из которых имеет линейную структуру из -мерные гиперплоскости, каждая из которых имеет линейную структуру из  -мерных гиперплоскостей... -мерных гиперплоскостей...
2.3. Евклидова структура (разновидность метрической структуры) указывает, как сравнивать длины отрезков, отложенных вдоль разных прямых. Для этого вводится теорема Пифагора (= евклидова метрика)
 Можно доказать, что при этом выполняется теорема Пифагора также для всех других ориентаций прямоугольного треугольника. Но сначала надо ввести понятие угла. Угол вводится именно теоремой косинусов: Можно доказать, что при этом выполняется теорема Пифагора также для всех других ориентаций прямоугольного треугольника. Но сначала надо ввести понятие угла. Угол вводится именно теоремой косинусов:
 Каждому косинусу однозначно соответствует угол в диапазоне Каждому косинусу однозначно соответствует угол в диапазоне ![$[0,\pi],$ $[0,\pi],$](https://dxdy-03.korotkov.co.uk/f/6/f/0/6f00e81ed69695b3882977f8f05e79aa82.png) а бо́льшие углы не используются как углы между прямыми, лучами, плоскостями и т. д. а бо́льшие углы не используются как углы между прямыми, лучами, плоскостями и т. д.
На самом деле, часто здесь пп. 2.2 и 2.3 формулируются иначе, в терминах векторов. Вектором в данном пространстве (это более узкий случай, чем векторы вообще) называется покоординатная разность двух точек -  -ок чисел. Такие векторы тоже будут -ок чисел. Такие векторы тоже будут  -ками чисел, но в другом пространстве - не в том, которое мы строим. Линейная структура соответствует векторной алгебре: сложение векторов и умножение их на числа, с соответствующими аксиомами. Они выполнятся, если векторы складывать между собой и умножать на числа покоординатно. Прямой линией становится множество всех векторов, пропорциональных данному, а между данными пропорциональными векторами можно найти отношение. Евклидова структура соответствует тому, что для векторов вводится евклидово скалярное произведение и евклидова норма: -ками чисел, но в другом пространстве - не в том, которое мы строим. Линейная структура соответствует векторной алгебре: сложение векторов и умножение их на числа, с соответствующими аксиомами. Они выполнятся, если векторы складывать между собой и умножать на числа покоординатно. Прямой линией становится множество всех векторов, пропорциональных данному, а между данными пропорциональными векторами можно найти отношение. Евклидова структура соответствует тому, что для векторов вводится евклидово скалярное произведение и евклидова норма:
 Длиной отрезка становится норма вектора, а углом - выражение Длиной отрезка становится норма вектора, а углом - выражение

Кроме того, можно ввести топологическую структуру после линейной и метрической структуры, и взять в качестве базы окрестностей точки не параллелепипеды, а шары радиусов 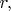 очерченные вокруг этой точки. Снова, в продвинутом курсе доказывается, что это будет та же самая топология. очерченные вокруг этой точки. Снова, в продвинутом курсе доказывается, что это будет та же самая топология. 3. В полученном пространстве вводятся некоторые симметрии. Пока в получившейся конструкции есть кое-что лишнее, "строительные леса". Это детали, которые унаследованы от способа построения пространства. Мы имеем некоторую "выделенную систему координат": начало координат  и оси координат и оси координат  Чтобы геометрия "не обращала на них внимание", надо сказать, что мы изучаем только те объекты, которые выдерживают некоторые преобразования, которые называются преобразованиями симметрии. В данном случае, это параллельные переносы, повороты, зеркальные отражения, и их всевозможные композиции - все вместе они называются движениями евклидовой геометрии. Фигуры, которые соответствуют друг другу после движения, называются в школе равными, а вообще-то конгруэнтными (поскольку они не равны одна другой как множества точек). Но понятно, что при таких движениях "теряется" расположение фигуры по отношению к системе координат. Чтобы геометрия "не обращала на них внимание", надо сказать, что мы изучаем только те объекты, которые выдерживают некоторые преобразования, которые называются преобразованиями симметрии. В данном случае, это параллельные переносы, повороты, зеркальные отражения, и их всевозможные композиции - все вместе они называются движениями евклидовой геометрии. Фигуры, которые соответствуют друг другу после движения, называются в школе равными, а вообще-то конгруэнтными (поскольку они не равны одна другой как множества точек). Но понятно, что при таких движениях "теряется" расположение фигуры по отношению к системе координат.
Преобразования симметрии не стоит вводить явным списком. Вместо этого, говорят, что преобразования симметрии - это те преобразования, которые сохраняют структуры, которые мы ввели: топологическую, линейную, евклидову. И получатся как раз те преобразования, что я перечислил: переносы, повороты, отражения и т.д.
Можно расширить множество симметрий, если сказать, что они должны сохранять меньше структур. Можно вводить другие структуры, и соответственно, им будут отвечать другие симметрии. Всё это уже выводит за рамки школьной геометрии. ---------------- С этой картиной в голове, можно понять, что: - можно использовать только теорему косинусов, если разрешить применять её к "вырожденным треугольникам" (расположенным по прямой линии); - можно эквивалентно использовать только векторную алгебру со скалярным произведением; - если не упоминать углы, то можно использовать только теорему Пифагора; - если не упоминать углы и длины, то можно обойтись векторной алгеброй без скалярного произведения. В общем, вы правильно понимаете, что теорема косинусов занимает одно из центральных мест в конструкции евклидовой геометрии. Хотя обычно всё-таки её заменяют на скалярное произведение, но это почти одно и то же.
|
|



