Если в числе

"много повторений" цифры

, то

- это "с хорошей точностью" степень десятки

(чуть меньше). Тогда

- это "с хорошей точностью"

, и в

"много повторений" цифры

.
Соответственно берем любое

, берем

, и получаем это свойство.
Соседние числа:

,
![$\sqrt[4]{124} = 3.336\ldots$ $\sqrt[4]{124} = 3.336\ldots$](https://dxdy-03.korotkov.co.uk/f/6/4/7/64779af18820dbf7d811c8c0cc02c4ab82.png)
,
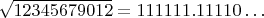
,
![$\sqrt[4]{12345679012} = 333.333333331\ldots$ $\sqrt[4]{12345679012} = 333.333333331\ldots$](https://dxdy-03.korotkov.co.uk/f/2/d/c/2dc847ecd7b08690bfbae3a7795449a282.png)
.