Ну давайте я несколько очень классических + элементарно формулируемых задач по аффинной алг.геометрии предложу.
0) Доказать, что любая бесконечная система полиномиальных уравнений с коэффициентами в

эквивалентна некоторой конечной подсистеме.
1) Доказать, что объединение трёх координатных осей в
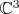
непредставимо в виде множетсва нулей системы из двух полиномиальных уравнений.
2) Доказать, что у кривой

нету рациональной параметризации.
3) Доказать что многочлен

не раскладывается в нетривиальное произведение двух многочленов с комплексными коэффициентами.
4) Доказать, что порождающая конуса

не может быть высечена на конусе одним рациональным уравнением в окрестности точки

первое что в голову пришло.