Поправьте меня если не прав, но по-моему уравнение 4-й степени тригонометрически не решабельно. Есть и другие формулы четверного угла, под которые замену подобрать тоже нереально.
Всё-таки решабельно.
Пусть есть уравнение

.
Его тригонометрическое решение такое:

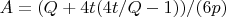



, где




(Проверка в Вольфраме)
{p, t} = RandomInteger[{-1000, 1000}, 2];
Print["\nEquation: ", p, "*x + x^4 = ", t, "\n"];
Print["Ordinary solution:"];
Print[x /. (p x + x^4 - t // NSolve) // Sort, "\n"];
Print["Trigonometric solution:"];
Q = ((-(27 p^4 + 128 t^3) + 3 (3 p^4 (27 p^4 + 256 t^3))^(1/2))/2)^(1/3);
A = (Q + 4 t (4 t/Q - 1))/(6 p);
B = (32 (3 p A + t))^(-1/6);
F = 256 B^12 t (16 A^4 + 2 A p - t);
R2 = Table[Cos[(ArcCos[1 + 8 F] + 2 \[Pi] j)/4], {j, 0, 3}];
R = 4 B^3 (1 - A^2);
y = (R2 - R)/(4 B^4);
Union[A + (1 + B y)^(1/2), A - (1 + B y)^(1/2)] // N // Sort
Использовалась формула черверного угла

.
Поскольку в замене

присутствует квадратный радикал, то сохранилась необходимость перебора знаков перед радикалом для отсечения лишних корней. Дробно-линейная замена дала бы точно четыре корня, но подобрать такую замену под формулу черверного угла у меня не получилось.