улучшение приближения параболической ломаной

[Paul Ivanov]

Имеется функция $g(x)$ - ломаная, соединяющая отрезками все пары точек вида $(k-1,(k-1)^2),(k, k^2)$ где $k \in \mathbb{N}$. Далее $\Delta(f)=\sup\limits_{x \in [0,+\infty)}|f(x)-g(x)|$.
Например, если $f(x)=x^2$, то $\Delta(f)=\frac{1}{4}$.
Вопрос заключается в том, существует ли всюду на $[0,+\infty)$ бесконечно дифференцируемая $f \in C^{(\infty)}$, такая, что для любого $k \in \mathbb{N}$ $f(k-1)=(k-1)^2$, чтобы при этом $\Delta(f)<\frac{1}{4}$?
Есть идея, как это опровергнуть с помощью искусственного построения функции путём соединения отрезков прямой с кусками других нелинейных бесконечно дифференцируемых функций, но надо это делать так, чтобы в точках соединения этих кусков функция оставалась бесконечно дифференцируемой, какие для этого надо подбирать нелинейные бесконечно дифференцируемые функции не очень понятно.

[vpb]

Существует, конечно. Вообще, бесконечная дифференцируемость --- довольно слабое условие. Между бесконечно дифференцируемыми функциями и непрерывными не такая уж большая разница. С другой стороны, между бесконечно дифференцируемыми и вещественно-аналитическими --- "дистанция огромного размера" (с).

Подумайте, в качестве промежуточного шага, над таким утверждением: для любого $\varepsilon>0$ существует функция $f$ на $[0,1]$, которая в некоторой окрестности (на $[0,1]$) точки $x=1$ --- тождественно нуль, в некоторой окрестности $0$ совпадает с $y=x$, везде внутри отрезка бесконечно дифференцируема, и $|f(x)|<\varepsilon$ $\forall x\in[0,1]$. А затем можно доказать, что непрерывную функцию на отрезке можно сколь угодно хорошо приблизить бесконечно дифференцируемой. И т.д. и т.п.

[vpb]

Еще более простое задание: состряпать функцию, бесконечно дифференцируемую на всей прямой, слева от нуля --- тождественный нуль, справа от 1 --- тождественно 1.

[Paul Ivanov]

Да, проверил, вы действительно правы. В таком случае, что если мы требование бесконечной дифференцируемости заменим на требование вещественной аналитичности? Всё равно можно будет построить функцию, удовлетворяющую новым требованиям и сколь угодно близко аппроксимирующую данную ломаную?

[ИСН]

Ну, полиномы Бернштейна-то никто не отменял.

[vpb]

ИСН
Многочлены Бернштейна касаются аппроксимации непрерывной функции многочленом на отрезке. Но приближение функции на отрезке многочленом и приближение непрерывной функции вещественно-аналитической на всей прямой --- это разные задачи.

Paul Ivanov
Да, любую непрерывную функцию на прямой можно приблизить вещественно-аналитической. Вот набросок рассуждения. Пусть $f\in C({\mathbb R})$.

1) Можно разложить $f$ в бесконечную сумму $f=\dots+g_{-1}+g_0+g_1+\ldots$, причем $g_i$ непрерывны, и $g_i=0$ вне отрезка $[i,\,i+2]$.

2) Пусть $g$ --- непрерывная функция на ${\mathbb R}$, $g=0$ вне $[0,2]$. Рассмотрим функции вида

$$h(x)=h_{A,C,n}(x) = C\sum_{k=1}^{n-1} g(2k/n)e^{-A(x-2k/n)^2}\,. $$

Тогда для любого $\varepsilon>0$ существуют $A$, $C$, $n$ такие, что $|h(x)-g(x)|<\varepsilon$ всюду на ${\mathbb R}$.

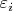
3) Пусть $\varepsilon>0$. Возьмем $\varepsilon_i>0$ такие, что $\sum_{i\in{\mathbb Z}}\varepsilon_i=\varepsilon$. Построим $h_i$ вышеуказанного вида, хорошо приближающие $g_i$ (с точностью $\varepsilon_i$), и возьмем их сумму. Это будет приближение для $f$, с точностью $\varepsilon$.

4) Отметим, что все $h_i$ --- вещественно-аналитические.

-- 12.02.2019, 18:46 --

5) Проблема теперь в том, чтобы показать, что бесконечная сумма $\sum_{i\in{\mathbb Z}} h_i$ тоже вещественно аналитическая. Это делается выходом в комплексную плоскость. Ясно, что все $h_i$ --- комплексно-аналитические. Теперь уточним пункт 2). Будем рассматривать нашу функцию $h$ в полосе $|\operatorname{Im} z|\leq 1/2$. Тогда при подходящих $A$, $n$ верно, что $|h(x)|<\varepsilon$ везде в этой полосе, за исключением прямоугольника $-1\leq \operatorname{Re} z\leq3$.
(т.е. $h$ не только хорошо приближает $g$ на действительной прямой, но и малО в полосе, за исключением "существенного" прямоугольника).
Отсюда следует, что $\sum h_i$ --- ряд аналитических функций, равномерно сходящийся на любом компакте в полосе. Поэтому его сумма --- аналитическая функция в полосе (лучше сказать голоморфная... короче, однозначная), значит ограничение этой суммы на ${\mathbb R}$ --- вещественно-аналитическая.