AnatolyBa, теперь уже всё нравится, но не просто "ненулевой", а "бесконечно большой" потенциал. Если там имеется хоть какой-то конечный заряд, то другого потенциала, кроме бесконечного, быть не может. Чисто по формуле потенциала. Возражений нет абсолютно.
А вот по поводу компенсации "непостоянного потенциала на поверхности" с помощью подбора заряда в центре инверсии - это
очень элегантный ход. Сейчас непременно попробую. Мне тоже этот путь казался лучшим, но я тогда не догадывался, что можно использовать заряд в центре инверсии. Получил неравномерное распределение потенциала (рисунок в прищепке) - и расстроился: неравномерный потенциал означал, что имеется касательная компонента напряжённости поля, следовательно, силовые линии не будут нормальны к поверхности, а в силу конформности "ненормальность" сохранилась бы и на исходной поверхности.
У того же Йосселя для расчёта мы придаём телу "заряд" (который уходит затем в центр инверсии), а потенциал вычисляем. Было жалко - как так, если мы заранее знаем, что на исходной поверхности потенциал всюду единица, почему не используем этот факт? Зато в приёме с компенсацией заряда он используется.
Прошу извинить за многословие. Это из-за радости, что туман рассеивается и приходит понимание.
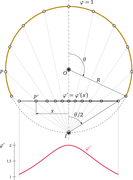
На рисунке (если кто-то заглянет сюда, не вдаваясь в подробности) - изображение шарового сегмента, жёлтая линия, заряженного до единичного потенциала; диск, полученный инверсией, чёрная линия; и отображение потенциала сегмента на этот диск, малиновый график. Центр инверсии отмечен символом

, центр кривизны сферического сегмента - символом

. Радиус инверсии равен радиусу кривизны сегмента. Построение полностью автоматическое, без ручного вмешательства.