Если я не ошибаюсь, считается, что континуум-гипотезу следует добавить к системе аксиом Цермело-Френкеля. А я уверен, что она опровергается и довольно просто. Оказывается, что можно выбрать такую нумерацию действительных чисел отрезка, что число, получаемое в результате диагональной процедуры, есть всего-навсего граница этого отрезка.
Постановка задачи.
Докажем, что множество вещественных чисел на отрезке [0,1] счётно. Поскольку множество вещественных чисел состоит из множества рациональных и множества иррациональных чисел, тем самым мы докажем, что счётное множество вещественных чисел больше несчётного множества иррациональных чисел. В результате получается противоречие, которое разрешается только в том случае, если континуум-гипотеза неверна, и несчётное множество вовсе не потому таково, что в нём слишком много элементов, чтобы их можно было считать, оно лишь плохо организовано для счёта.
Попутно покажем, что диагональная процедура Георга Кантора вовсе не годится для доказательства того, что существуют множества, содержащие слишком много элементов, чтобы их можно было сосчитать.
Доказательство.
Мы будем пользоваться двоичной системой. Однако, нумеровать числа будем так, чтобы яснее показать несостоятельность диагонального доказательства Георга Кантора.
Всякое вещественное число на отрезке [0,1] можно представить бесконечной двоичной дробью, в которой слева от точки находится нуль.


Среди рассматриваемых чисел найдутся такие, в которых справа имеется бесконечная последовательность из нулей или единиц. Эти числа, естественно, могут быть записаны с конечным количеством значащих цифр и с необязательным добавлением справа нуля в скобках, означающим бесконечную последовательность нулей.


где двоичные знаки

могут принимать значения 0 или 1, а двоичный знак

только значение 1.
Вещественное число нуль сопоставим с числом нуль из множества натуральных чисел.
Сопоставление остальных чисел множества вещественных чисел с числами множества натуральных чисел начнём с числа, представленного одной значащей цифрой после двоичной точки. Это число:

или

, которое мы и поставим в соответствие с натуральным числом 1.
Теперь переходим к числам, которые представлены двумя цифрами после двоичной точки. Таких чисел окажется

:
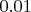
и

. Они получат номера

и

.
Аналогичным образом пронумеруем числа с тремя цифрами после точки. (Заметим попутно, что нет никакой необходимости продолжать диагональную процедуру бесконечно, как это делает профессор Зенкин). Таких чисел будет

:

,

,

,

. Они получат номера от

до

.
Чисел с 4-мя цифрами после точки будет

:

,

,

,

,

,

,

,

. Они получат номера от

до

. После этого будем нумеровать числа с 5-ю, 6-ю, 7-ю и так далее значащими цифрами после точки.
Теперь посмотрим, что за число получается в результате диагонального метода Георга Кантора. С этой целью выпишем несколько первых чисел из нашей нумерации.
0 - 0.

00000000000000000
1 - 0.1

0000000000000000
2 - 0.01

000000000000000
3 - 0.110

00000000000000
4 - 0.0010

0000000000000
5 - 0.01100

000000000000
6 - 0.101000

00000000000
7 - 0.1110000

0000000000
8 - 0.00010000

000000000
9 - 0.001100000

00000000
10 0.0101000000

0000000
11 0.01110000000

000000
12 0.100100000000

00000
13 0.1011000000000

0000
14 0.11010000000000

000
15 0.111100000000000

00
В этих числах особо выделены цифры, стоящие на диагонали. Это те самые цифры, которые по методу Георга Кантора следует изменить, чтобы получить число, которого нет в нашей последовательности.
Поскольку на диагонали только нули, то результатом диагонального метода Георга Кантора окажется число, в котором, справа от точки будет бесконечный ряд единиц:

или

. Иначе говоря результатом диагонального метода Георга Кантора окажется правая граница отрезка [0,1].
Итак, мы показали, что все числа отрезка [0,1] можно поставить в соответствие числам натурального ряда. Множество вещественных (действительных) чисел счётно.
Что и требовалось доказать.
Выводы.
Континуум-гипотеза несостоятельна. Диагональную процедуру некорректно использовать для доказательства несчётности вещественных чисел. Несчётное множество таково не потому, что содержит слишком много элементов, оно лишь плохо организовано для счёта. Мощность континуума не отличается от мощности множества натуральных чисел. Следовательно, нет оснований для иерархии мощностей и трансфинитных чисел. Следовательно, нет оснований для раскола по вопросам оснований математики. Наоборот, есть почва для объединения математиков всех воззрений. А вместо системы аксиом ZFC математики уже объединёнными усилиями должны разработать систему, более адекватную математической действительности.



