Размерность пространства решений СЛАУ

[RichPeach]

Имеется однородная СЛАУ 5-го порядка с матрицей

$$ A=\begin{pmatrix} 2 & 3 & b+2 & 8 & 3 \\ -1 & 3 & 1 & 4 & 1 \\ 1 & 4-a & 3 & 9 & 4 \\ 2 & 2 & 1 & 5 & 3 \\ 4 & 2 & 0 & 4 & 6 \end{pmatrix} $$

Необходимо определить параметры $a$ и $b$, при которых размерность пространства решений данной СЛАУ будет максимальна. Это равносильно тому, что ранг матрицы будет минимален. Методом окаймляющих миноров я показал, что $\mathrm{rang}\,A\geqslant4$. Нам нужен минимальный ранг, $\mathrm{rang}\,A=4$, следовательно, единственный минор пятого порядка (определитель матрицы) должен быть равен нулю.

$$\det A=\begin{vmatrix} 2 & 3 & b+2 & 8 & 3 \\ -1 & 3 & 1 & 4 & 1 \\ 1 & 4-a & 3 & 9 & 4 \\ 2 & 2 & 1 & 5 & 3 \\ 4 & 2 & 0 & 4 & 6 \end{vmatrix}=30(a+1)b=0$$

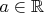
Откуда $a=-1$, $b\in\mathbb{R}$ или $b=0$, $a\in\mathbb{R}$. Упускаю ли я что-то, или ответ всё же правильный? В этой задаче в ответ необходимо было указать $a+b$. Насколько я понимаю, это невозможно, но в ответе я указал пересечение решений $a=-1$, $b=0$, $a+b=-1$. Оказалось, неправильно. Или требовать в ответ $a+b$ некорректно?

[TOTAL]

А вдруг просто определитель неправильно нашли?

[Pphantom]

TOTAL в сообщении #1362351 писал(а):

А вдруг просто определитель неправильно нашли?

Нет, он действительно такой.

[svv]

RichPeach в сообщении #1362318 писал(а):

$$\det A=\begin{vmatrix} 2 & 3 & b+2 & 8 & 3 \\ -1 & 3 & 1 & 4 & 1 \\ 1 & 4-a & 3 & 9 & 4 \\ 2 & 2 & 1 & 5 & 3 \\ 4 & 2 & 0 & 4 & 6 \end{vmatrix}=30(a+1)b$$

Вычисляя определитель, можно элементарными преобразованиями (не меняющими ранг) привести матрицу $A$ к матрице
$B=\begin{bmatrix}a+1 & 0 & 0 & 0 & 0 \\0 & b & 0 & 0 & 0 \\0 & 0 & 1 & 0 & 0 \\0 & 0 & 0 & 1 & 0 \\0 & 0 & 0 & 0 & 1\end{bmatrix}$
И каков минимальный ранг $B$ ?

[TOTAL]

svv в сообщении #1362573 писал(а):

RichPeach в сообщении #1362318 писал(а):

$$\det A=\begin{vmatrix} 2 & 3 & b+2 & 8 & 3 \\ -1 & 3 & 1 & 4 & 1 \\ 1 & 4-a & 3 & 9 & 4 \\ 2 & 2 & 1 & 5 & 3 \\ 4 & 2 & 0 & 4 & 6 \end{vmatrix}=30(a+1)b$$

Вычисляя определитель, можно элементарными преобразованиями (не меняющими ранг) привести матрицу $A$ к матрице
$B=\begin{bmatrix}a+1 & 0 & 0 & 0 & 0 \\0 & b & 0 & 0 & 0 \\0 & 0 & 1 & 0 & 0 \\0 & 0 & 0 & 1 & 0 \\0 & 0 & 0 & 0 & 1\end{bmatrix}$
И каков минимальный ранг $B$ ?

При $a+1=0$ вычеркиваем первую строку и первый столбец

$$\det A=\begin{vmatrix} 3 & 1 & 4 & 1 \\ 5 & 3 & 9 & 4 \\ 2 & 1 & 5 & 3 \\ 2 & 0 & 4 & 6 \end{vmatrix}=28$$

[RichPeach]

Согласен с TOTAL, но ответа $a+b=-1$ (который почему-то оказался неправильным) это не меняет. svv, Вы преобразовывали матрицу построчно? Как понимаете, это важный момент.

[svv]

Вы правы, я ошибся. Можно преобразовать лишь к виду
$B=\begin{bmatrix}a+1 & 1 & 0 & 0 & 0 \\0 & b & 0 & 0 & 0 \\0 & 0 & 1 & 0 & 0 \\0 & 0 & 0 & 1 & 0 \\0 & 0 & 0 & 0 & 1\end{bmatrix}$
Единичка (элемент $b_{12}$) не влияет на определитель, но влияет на минимальный ранг.

-- Чт дек 20, 2018 16:35:59 --

RichPeach в сообщении #1362717 писал(а):

который почему-то оказался неправильным

Вы получили, что минимальный ранг 4 достигается при выполнении любого из условий $a+1=0, b=0$, при этом $a+b$ можно сделать любым.

[RichPeach]

Да, я как раз об этом и написал в своём вопросе. В этом и проблема. В ответ должно было пойти обязательно конкретное число, вводимое с клавиатуры. Отсюда вопрос: корректно ли составлена задача, то есть форма ответа? Требуют конкретного ответа, который получить невозможно!

[svv]

Ответ, который Вы предложили, $-1$, во всяком случае не хуже любого другого вещественного числа. Но система его забраковала. Это показывает, что задача + требования к вводу ответа + система ввода и проверки ответа — всё это вместе некорректно.