Здравствуйте. Меня терзают сомнения по поводу простых вещей по "социальным" причинам. Либо я сильно туплю, либо вопрос тривиальный. Спасибо.
Я тут решал требуемые задачки. Для

-групп используется нетривиальность центра и то, что центр содержит подгруппу порядка

- как абелева

-группа. У меня такое ощущение, что условие абелевости излишнее. Пусть
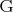
-

-группа. Пусть порядок
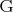
равен

,

. Если
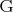
- циклическая, то утверждение выполняется для
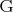
. Пусть
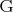
- не циклическая, тогда рассмотрим

,

,


,

. Тогда

содержит подгруппу порядка

, которая будет подгруппой
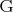
.



