EUgeneUS,
В Студопедии глупости пишут и рисуют странные картинки, и вводят Вас в заблуждение. Например, всё написанное в Студопедии не годится для случая идеальных контуров или тороидальной катушки.
Потокосцепление контура 
— это суммарный поток проходящий через контур, формируемый как самим контуром, так и другими связными с ним контурами.

У каждого контура, в системе связных контуров, своё потокосцепление

, то есть различные контуры могут сцеплять (пропускать через себя) различное количество потока.
Для определения индуктивности системы связных контуров, нас интересует суммарное потокосцепление:

Для системы идеальных, полностью связных контуров их потокосцепления равны,

, то суммарное потокосцепление системы идеальных контуров:


Так как потокосцепление отдельного контура:




где
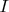
— это ток через отдельный идеальный контур, или ток по системе тороидальных катушек, а

— индуктивность отдельного (несвязного, изолированного от других) контура.



