Спасибо за ответы! Итак, утверждение неверно. Я слишком обобщил. Спасибо высказавшимся, вы помогли мне понять, где я заблуждался.
Изначально мне хотелось посчитать индекс "поля единичных векторов" с помощью интегрирования какой-то не очень понятной формы
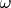
, живущей в тотальном пространстве расслоения единичных векторов. Поэтому меня заинтересовало следующее утверждение, являющееся частным случаем неверного утверждения из первого поста:
(Оффтоп)
Пусть

--

-мерная сфера,

--

-мерный шар (радиуса

),
![$v:B\setminus \{0\}=S\times(0,1]\to S$ $v:B\setminus \{0\}=S\times(0,1]\to S$](https://dxdy-01.korotkov.co.uk/f/0/b/f/0bf9028ea9eb4ade911ac83c7b9e94f282.png)
-- гладкое отображение,
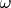
--

-форма на

. Обозначим, как раньше,

сужение

на

,

(степень не зависит от

, поскольку они гомотопны). Обозначим

вложение

как сферы радиуса

с тем же центром, что и у шара

.
Рассмотрим теперь 2 отображения из

в

, а именно

и

(где первый

обозначает отображение

в центр шара

).
Верно ли, что 
?
Скорее всего, это тоже неверно. Впрочем, мне для вычисления индекса это неважно, потому что

можно изменить так, чтобы, например,

имело предел при

(например, положить

при

). Для такого специального поля

вышеприведённое утверждение будет верно, а индекс не поменяется.
Ниже следует неудачная попытка (её я упоминал в 1-м посте) доказать вышеприведённое утверждение для произвольного

в случае 1-мерной

. Теперь я не верю, что из этой попытки что-то путное получится, но она уже записана и, может быть, будет кому-нибудь интересна.
(Оффтоп)
Итак,
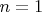
. Пусть

-- угловая координата на

,

-- координаты на

(то есть

рассматриваем как подмножество плоскости, заданное неравенством

, а

-- угловая координата на множителе-окружности),

, отображение

переводит

,

.
Нужно посчитать

![$=\int\limits_S d\alpha\left[-\omega_x(r\cos\alpha, r\sin\alpha,v_r(\alpha))r\sin\alpha + \omega_y(...)r\cos\alpha+\omega_\varphi(...)v_r' (\alpha) \right ]$ $=\int\limits_S d\alpha\left[-\omega_x(r\cos\alpha, r\sin\alpha,v_r(\alpha))r\sin\alpha + \omega_y(...)r\cos\alpha+\omega_\varphi(...)v_r' (\alpha) \right ]$](https://dxdy-03.korotkov.co.uk/f/6/7/2/672d05e4ebf107641263aa4d0fedd09782.png)
.
Интеграл от первых 2 членов стремится к

, потому что при

они равномерно сходятся к

(
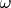
определена на компактном множестве, поэтому её коэффициенты равномерно ограничены по модулю). Разберёмся с 3-м членом.
Пусть

-- это множество критических значений отображения

. Оно замкнуто, так как всё компактно. Тогда

-- это объединение непересекающихся интервалов

(считаем, что

непусто, но это несущественно). По теореме Сарда это объединение имеет полную меру.
Прообраз каждого интервала

относительно

состоит из конечного количества интервалов

. Обозначим

сужение

на такой интервал; это диффеоморфизм на

. Поэтому

. Каждый интеграл в этом выражении сходится к интегралу от

(ограничим на большой отрезок в

, на отрезке сходимость будет почему-то там равномерная, а интеграл по остатку маленький, потому что коэффициенты
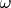
равномерно ограничены).
А дальше плохо. Если бы

было замкнуто, то можно было бы рассматривать его вместо

и переходить к пределу

во всей сумме, и всё бы получилось, так как оно разбивало бы окружность на интервалы, объединение которых имело бы полную меру. Однако

может быть не только не замкнутым, а хоть даже всюду плотным (можно выбрать

так, чтобы у него было конечное количество каких угодно критических значений, и проинтерполировать).
Ещё можно было бы написать

и пытаться оценить модуль разности, но тут тоже ничего не получится, потому что хотя при фиксированном

индекс

пробегает только конечное множество значений, но на количество этих знчений никакого ограничения нет: можно выбрать

так, что их будет сколько угодно, и проинтерполировать...



