Задача по геометрии по мотивам задачи 6 IMO-2018

[grizzly]

vvsss в сообщении #1348857 писал(а):

Мнение grizzly о моих умственных способностях

Я лишь высказал своё мнение о Вашем поведении на форуме, а не о способностях (см. цитату, на которую я реагировал).

vvsss в сообщении #1348857 писал(а):

Директрисы покажутся как только возникнет идея у кого-то из исследователей.

Вряд ли кто-то станет теперь рисовать директрисы, после того, как есть фокусы и хоть одна точка эллипса. Слишком уж тривиальная задача.

vvsss
А за тему спасибо. Как бы там ни было, благодаря Вам пару дней мы следили за интереснейшим развитием событий. К тому же узнали что-то новое и интересное об эллипсах (я посмотрел, что даже в англовики об этом не рассказано). Теперь гугло-поиск поможет каждому интересующемуся найти эту тему.

[wrest]

vvsss в сообщении #1348857 писал(а):

Моя ошибка, связанная с неединственностью решения вызвала на мой взгляд очень интересную дискуссию,

Да, задачка интересная.

vvsss в сообщении #1348857 писал(а):

Информация о построении, которую участники форума поняли, выкладывается оперативно и не засекречивается.

Ну не знаю, из ваших рисунков лично мне ничего не ясно, я не вижу как построены фокусы и точка касания. При этом две фразы DeBill практически полностью раскрыли вопрос.

vvsss в сообщении #1348857 писал(а):

Работа wrest меня просто восхищает.

Осваивайте геогебру, там картинки красивые можно делать. Автокад (это же автокад?) для этого не очень приспособлен ;)

[vvsss]

Мнение заслуженного участника grizzly является для человека, зашедшего на сайт впервые после лет десяти лет отсутствия,
слабо владеющего интернетом, не знающего толком правила сайта, критерием справедливости.
Спасибо за приветливую встречу.
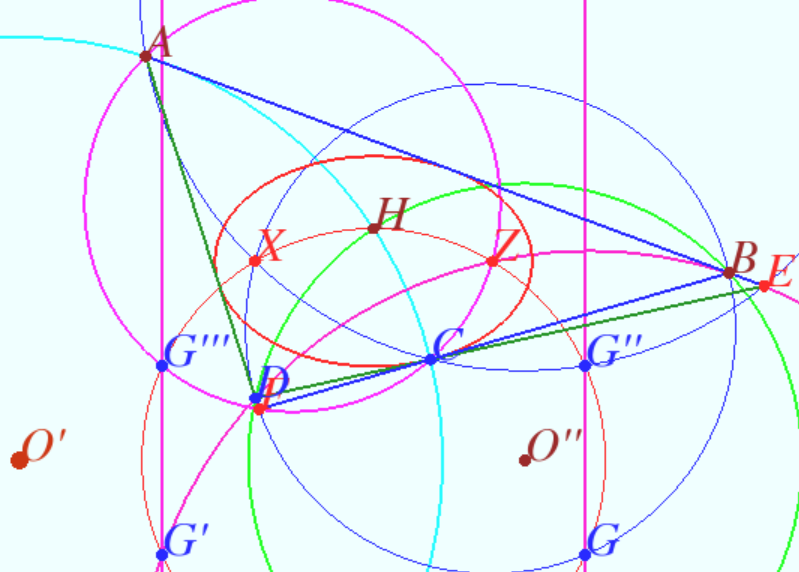
Публикую построение, так как теперь тема стала не интересной, и надеюсь что доказательство будет теперь очевидно,
по крайней мере заслуженному участнику grizzly.
Я строил доказательство с использованием инверсии.
Эллипс, как уже сказали участники, нарисован для красоты.
И закроем тему.

-- Ср окт 24, 2018 20:13:23 --

Уважаемый wrest.
Это программа ginma.
О ней позитивно отзывались на конференциях ICGG, ATCM и других.
Она более мощная, чем геогебра, даёт больше возможностей за исключением построения следов. Это мы не сделали, а так как она не нашла широкого распространения, работы над ней прекращены.
Обычно её запрашивали отдельные геометры, как правило молодые, но в публикациях я её не видел.
Пример сложного рисунка сейчас постараюсь прикрепить.

[wrest]

vvsss
Вместо того чтобы дуться, лучше бы описали построение.
Что у вас за $O', O? Окружность которая проходит через фокусы как построена? Куда делась точка касания $K$, теперь $C$ вместо неё? Во что вообще эллипс вписан? Больше похоже на то, что в треугольник, я по крайней вижу три точки касания а не четыре...

-- 24.10.2018, 20:22 --

vvsss в сообщении #1348870 писал(а):

Она более мощная, чем геогебра, даёт больше возможностей

Может быть, но выглядит... не очень. Это во-первых, а во-вторых, геогебра есть у всех потому что она онлайн, и в ней есть механизмы как поделиться собственно чертежом, что в нашей ситуации иногда бывает полезно.

-- 24.10.2018, 20:26 --

vvsss в сообщении #1348870 писал(а):

И закроем тему.

Так вы собсно построения так и не дали. Интересен ваш способ, я бы может попробовал повторить, но ничего ж не описано...

[grizzly]

vvsss

(Оффтоп)

Не серчайте, пожалуйста. Я приношу свои извинения -- я был излишне раздражён тем, что Вы не объясняете ни ваших рисунков, ни мотивов их опубликования. Из-за этого неправильно понял другие Ваши высказывания. Вашего решения я пока не понял, но это не так уж важно.

[vvsss]

Длинный эллипсоид пересекает сферу. Сложность была в том,
что меня попросили построить кривую пересечения, которая интерактивно изменяется и может распадаться на две области при изменении параметров сферы. Показан переходный момент. Рисунок урезан из-за требования 800 пикселей.

[vvsss]

Точки O', O'' это центры окружностей Аполлония о которых уже писали решавшие и которые известно как найти.
Все остальные построения это окружности через три точки, прямые через две точки, и точки их пересечения.
Здесь Ваша квалификация вполне достаточна. Для меня проблема была в доказательстве.
Прямые АВ и СD пересекаются в Е
Прямые AD и ВС пересекаются в F.
Окружности АСЕ и BDF пересекаются в фокусе Х
Окружности АСF и BDE пересекаются в фокусе Z
H - точка пересечения окружностей Аполлония
Окружность XHZ пересекает АСЕ, BDF, ACF, BDE в точках, принадлежащих директрисам.
Мне казалось, что это очевидно из рисунка.

[wrest]

vvsss
У вас $C$ лежит на $BD$, судя по картинке. Угол $\angle BCD=180^{\circ}$, четырехугольника нет. И где точка касания?

[vvsss]

Уважаемый wrest
Пожалуйста, воспользуйтесь геогеброй, выполните построения и проверьте, что все получится.
Если математик Вашего уровня видит точку Е не на прямой ВС, он догадывается, что угол не 180.
Впечатление, что под Вашим ником пишет кто-то новый.
Вы блестяще выполнили исследование фокусов, Вы нашли такой изумительный экстремум в задаче про уточку
и вдруг говорите о 180...
Идиотское ограничение 800 пикселей по ширине рисунка принудило меня сдвинуть точки.
На предыдущих рисунках, где было меньше информации, четырёхугольник был очевиден.

[wrest]

vvsss
Я совсем не математик, вообще. Я дилетант
Математики тут grizzly и DeBill

Хорошо, попробую.

[wrest]

vvsss в сообщении #1348905 писал(а):

Прямые АВ и СD пересекаются в Е
Прямые AD и ВС пересекаются в F.
Окружности АСЕ и BDF пересекаются в фокусе Х
Окружности АСF и BDE пересекаются в фокусе Z

Да, фокусы строятся норм. Если произведения противоположных сторон не равны, то не строятся.

vvsss в сообщении #1348905 писал(а):

H - точка пересечения окружностей Аполлония

Как строим эти окружности?

-- 25.10.2018, 10:37 --

Ещё новости из жизни эллипсов.

Оказалось, что эллипс, построенный по методу vvsss, по площади иногда меньше, а иногда больше, чем построенный по методу "диагоналей" на четырехугольнике со сторонами $1,5:3:4:2$

Вообще, как мне кажется, задача далека от завершения :)

Еще хотелось бы научиться, если дан произвольный выпуклый четырехугольник (ну, можно конечно ограничить: нет параллельных сторон; или все стороны различны):
1. Строить вписанный эллипс (фокусы и точки касания) максимальной площади.
2. Строить фокусы вписанного эллипса по данной точке касания на одной из сторон (а такой эллипс - единственный).
3. Дополнительно к пункту 2 -- строить второй вписанный эллипс (фокусы и точки касания) равный по площади построенному по пункту 2 (вероятно, такой всегда существует и только один, если только в пункте 2 уже не выбран эллипс максимальной площади).

[vvsss]

1. Дан выпуклый четырёхугольник ABCD у которого произведения противоположных сторон равны.
2. Проводим диагональ АС и срединный перпендикуляр к отрезку BD.
3. Точка пересечения этих прямых и является центром искомой окружности.
Для построения выпуклого четырёхугольника ABCD в общем случае
используйте знаменитую программу геогебра.

Задача из раздела "Помогите решить" полностью завершена так как
1. Любой пользователь по приведенному алгоритму может построить фокусы и директрисы
для произвольного четырёхугольника общего вида.
2. Автор знает, как доказать, что это построение корректно.
Другие задачи автор данной задачи не ставил.

[wrest]

vvsss в сообщении #1348905 писал(а):

Прямые АВ и СD пересекаются в Е
Прямые AD и ВС пересекаются в F.
Окружности АСЕ и BDF пересекаются в фокусе Х
Окружности АСF и BDE пересекаются в фокусе Z

Тут требуется уточнение: Если $ABCD$ трапеция, то одна из точек $E$ или $F$ не существует, тогда просто проводим прямую: если не существует $F$, то вместо окружностей $ACF$ и $BDF$ проводим прямые $AC$ и $BD$ (диагонали).

-- 25.10.2018, 10:56 --

vvsss в сообщении #1349004 писал(а):

1. Любой пользователь по приведенному алгоритму может построить фокусы и директрисы
для произвольного четырёхугольника общего вида.

По вашему алгоритму - нет, не может. Ваш алгоритм работает только если произведения противоположных сторон равны.

-- 25.10.2018, 10:57 --

vvsss в сообщении #1349004 писал(а):

Задача из раздела "Помогите решить" полностью завершена

Ok, замолкаю тогда в этой теме.

[vvsss]

Уважаемый wrest.
Я ставил задачу только для такого четырёхугольника, у которого произведения противоположных сторон равны.
Поэтому по моему алгоритму фокусы и директрисы строятся всегда.
В вырожденных случаях центр окружности уходит на бесконечность, окружность становится прямой,
но я считал это тривиальным.
В математике принято ограничиваться решением задачи в рамках условия, что в данном случае выполнено.
Спасибо за интересное взаимодействие.